This chapter was published as Uruñuela et al. (2023).
Deconvolution of the hemodynamic response is an important step to access short timescales of brain activity recorded by functional magnetic resonance imaging (fMRI). Albeit conventional deconvolution algorithms have been around for a long time (e.g., Wiener deconvolution), recent state-of-the-art methods based on sparsity-pursuing regularization are attracting increasing interest to investigate brain dynamics and connectivity with fMRI. This chapter describes the principles of hemodynamic deconvolution in fMRI, and revisits the main concepts underlying two main sparsity-promoting deconvolution algorithms, Paradigm Free Mapping and Total Activation, in an accessible manner. Despite their apparent differences in the formulation, these methods are shown theoretically equivalent as they represent the synthesis and analysis sides of the same problem, respectively. This chapter demonstrates this equivalence in practice with their best-available implementations using both simulations, with different signal-to-noise ratios, and experimental fMRI data acquired during a motor task and resting-state. The chapter also evaluates the parameter settings that lead to equivalent results, and showcases the operation of these algorithms in comparison with Coactivation Pattern analysis. This note is useful for practitioners interested in gaining a better understanding of state-of-the-art hemodynamic deconvolution, and aims to answer questions regarding the differences between the two methods.
Introduction¶
Functional magnetic resonance imaging (fMRI) data analysis is often directed to identify and disentangle the neural processes that occur in different brain regions during task or at rest. As the blood oxygenation level-dependent (BOLD) signal of fMRI Ogawa et al., 1990 is only a proxy for neuronal activity mediated through neurovascular coupling Logothetis et al., 2001, an intermediate step that estimates the activity-inducing signal, at the timescale of fMRI, from the BOLD timeseries can be useful. Conventional analysis of task fMRI data relies on the general linear models (GLM) to establish statistical parametric maps of brain activity by regression of the empirical timecourses against hypothetical ones built from the knowledge of the experimental paradigm Boynton et al., 1996Cohen, 1997Friston et al., 1998Friston et al., 2008. However, timing information of the paradigm can be unknown, inaccurate, or insufficient in some scenarios such as naturalistic stimuli, resting-state, or clinically-relevant assessments.
Deconvolution and methods alike are aiming to estimate neuronal activity by undoing the blurring effect of the hemodynamic response, characterized as a hemodynamic response function (HRF)[1]. Given the inherently ill-posed nature of hemodynamic deconvolution, due to the sluggish characteristics of the HRF, the key is to introduce additional constraints in the estimation problem that are typically expressed as regularization terms. For instance, the so-called Wiener deconvolution is expressing a “minimal energy” constraint on the deconvolved signal, and has been used in the framework of psychophysiological interaction analysis to compute the interaction between a seed’s activity-inducing timecourse and an experimental modulation Glover, 1999Gitelman et al., 2003Gerchen et al., 2014Di & Biswal, 2018Freitas et al., 2020. Complementarily, the interest in deconvolution has increased to explore time-varying activity in resting-state fMRI data Preti et al., 2017Keilholz et al., 2017Lurie et al., 2020Bolton et al., 2020. In that case, the aim is to gain better insights of the neural signals that drive functional connectivity at short time scales, as well as learning about the spatio-temporal structure of functional components that dynamically construct resting-state networks and their interactions Karahanoğlu & Van De Ville, 2017.
Deconvolution of the resting-state fMRI signal has illustrated the significance of transient, sparse spontaneous events Petridou et al., 2013Allan et al., 2015 that refine the hierarchical clusterization of functional networks Karahanoğlu et al., 2013 and reveal their temporal overlap based on their signal innovations not only in the human brain Karahanoğlu & Van De Ville, 2015, but also in the spinal cord Kinany et al., 2020. Similar to task-related studies, deconvolution allows to investigate modulatory interactions within and between resting-state functional networks Di & Biswal, 2013Di & Biswal, 2015. In addition, decoding of the deconvolved spontaneous events allows to decipher the flow of spontaneous thoughts and actions across different cognitive and sensory domains while at rest Karahanoğlu & Van De Ville, 2015Gonzalez-Castillo et al., 2019Tan et al., 2017. Beyond findings on healthy subjects, deconvolution techniques have also proven its utility in clinical conditions to characterize functional alterations of patients with a progressive stage of multiple sclerosis at rest Bommarito et al., 2021, to find functional signatures of prodromal psychotic symptoms and anxiety at rest on patients suffering from schizophrenia Zoeller et al., 2019, to detect the foci of interictal events in epilepsy patients without an EEG recording Lopes et al., 2012Karahanoglu et al., 2013, or to study functional dissociations observed during non-rapid eye movement sleep that are associated with reduced consolidation of information and impaired consciousness Tarun et al., 2021.
The algorithms for hemodynamic deconvolution can be classified based on the assumed hemodynamic model and the optimization problem used to estimate the neuronal-related signal. Most approaches assume a linear time-invariant model for the hemodynamic response that is inverted by means of variational (regularized) least squares estimators Glover, 1999Gitelman et al., 2003Gaudes et al., 2010Gaudes et al., 2012Gaudes et al., 2013Caballero-Gaudes et al., 2019Hernandez-Garcia & Ulfarsson, 2011Karahanoğlu et al., 2013Cherkaoui et al., 2019Hütel et al., 2021Costantini et al., 2022, logistic functions Bush & Cisler, 2013Bush et al., 2015Loula et al., 2018, probabilistic mixture models Pidnebesna et al., 2019, convolutional autoencoders Hütel et al., 2018 or nonparametric homomorphic filtering Sreenivasan et al., 2015. Alternatively, several methods have also been proposed to invert non-linear models of the neuronal and hemodynamic coupling Riera et al., 2004Penny et al., 2005Friston et al., 2008Havlicek et al., 2011Aslan et al., 2016Madi & Karameh, 2017Ruiz-Euler et al., 2018.
Among the variety of approaches, those based on regularized least squares estimators have been employed more often due to their appropriate performance at small spatial scales (e.g., voxelwise). Relevant for this work, two different formulations can be established for the regularized least-squares deconvolution problem, either based on a synthesis- or analysis-based model Elad et al., 2007Ortelli & Geer, 2019. On the one hand, Paradigm Free Mapping is based on a synthesis formulation that is solved by means of regularized least-squares estimators such as ridge-regression Gaudes et al., 2010 or LASSO Gaudes et al., 2013. The rationale of the synthesis-based model is that we know or suspect that the true signal (here, the neuronally-driven BOLD component of the fMRI signal) can be represented as a linear combination of predefined patterns or dictionary atoms (for instance, the hemodynamic response function). On the other hand, Total Activation is based on a analysis formulation that is solved with a regularized least-squares estimator using generalized total variation Karahanoglu et al., 2011Karahanoğlu et al., 2013. The rationale of the analysis-based approach considers that the true signal is analyzed by some relevant hemodynamic operator Khalidov et al., 2011 and the resulting signal is sparse in time.
The users of these algorithms have often questioned about the similarities and differences between the two methods and which one is better. To clarify this point, this chapter initially presents the theory behind these two deconvolution approaches: Paradigm Free Mapping (PFM) Gaudes et al., 2013 -- available in AFNI as 3dPFM[2] and 3dMEPFM[3] for single-echo and multi-echo data, respectively -- and Total Activation (TA) Karahanoğlu et al., 2013 -- available as part of the iCAPs toolbox[4]. The chapter describes the similarities and differences in their analytical formulations, and how they can be related to each other. Next, their performance is assessed controlling for a fair comparison on simulated and experimental data. Finally, the chapter discusses their benefits and shortcomings and conclude with our vision on potential extensions and developments.
Theory¶
Notations and Definitions¶
Matrices of size rows and columns are denoted by boldface capital letters, e.g., , whereas column vectors of length are denoted as boldface lowercase letters, e.g., . Scalars are denoted by lowercase letters, e.g., . Continuous functions are denoted by brackets, e.g., , while discrete functions are denoted by square brackets, e.g., . The Euclidean norm of a matrix is denoted as , the -norm is denoted by and the Frobenius norm is denoted by . The discrete integration () and difference () operators are defined as:
General Linear Model Analysis¶
A conventional general linear model (GLM) analysis puts forward a number of regressors incorporating the knowledge about the paradigm or behavior. For instance, the timing of epochs for a certain condition can be modeled as an indicator function (e.g., Dirac functions for event-related designs or box-car functions for block-designs) convolved with the hemodynamic response function (HRF) , and sampled at the repetition time (TR) resolution Friston et al., 1994Friston et al., 1998Boynton et al., 1996Cohen, 1997:
The vector then constitutes the regressor modelling the hypothetical response, and several of them can be stacked as columns of the design matrix , leading to the well-known GLM formulation:
where the empirical timecourse is explained by a linear combination of the regressors in weighted by the parameters in and corrupted by additive noise . Under independent and identically distributed Gaussian assumptions of the latter, the maximum likelihood estimate of the parameter weights reverts to the ordinary least-squares estimator; i.e., minimizing the residual sum of squares between the fitted model and measurements. The number of regressors is typically much less than the number of measurements , and thus the regression problem is over-determined and does not require additional constraints or assumptions Henson & Friston, 2007.
In the deconvolution approach, no prior knowledge of the hypothetical response is taken into account, and the purpose is to estimate the deconvolved activity-inducing signal from the measurements , which can be formulated as the following signal model
where is a Toeplitz matrix that represents the discrete convolution with the HRF, and is a length- vector with the unknown activity-inducing signal. Note that the temporal resolution of the activity-inducing signal and the corresponding Toeplitz matrix is generally assumed to be equal to the TR of the acquisition, but it could also be higher if an upsampled estimate is desired. Despite the apparent similarity with the GLM equation, there are two important differences. First, the multiplication with the design matrix of the GLM is an expansion as a weighted linear combination of its columns, while the multiplication with the HRF matrix represents a convolution operator. Second, determining is an ill-posed problem given the nature of the HRF. As it can be seen intuitively, the convolution matrix is highly collinear (i.e., its columns are highly correlated) due to large overlap between shifted HRFs (see C), thus introducing uncertainty in the estimates of when noise is present. Consequently, additional assumptions under the form of regularization terms (or priors) in the estimate are needed to reduce their variance. In the least squares sense, the optimization problem to solve is given by
The first term quantifies data fitness, which can be justified as the log-likelihood term derived from Gaussian noise assumptions, while the second term brings in regularization and can be interpreted as a prior on the activity-inducing signal. For example, the -norm of (i.e., ) is imposed for ridge regression or Wiener deconvolution, which introduces a trade-off between the data fit term and “energy” of the estimates that is controlled by the regularization parameter λ. Other well-known regularized terms are related to the elastic net (i.e., ) Zou & Hastie, 2005.
Paradigm Free Mapping¶
In Paradigm Free Mapping (PFM), the formulation of Eq. 5 was considered equivalently as fitting the measurements using the atoms of the HRF dictionary (i.e., columns of ) with corresponding weights (entries of ). This model corresponds to a synthesis formulation. In Gaudes et al. (2013) a sparsity-pursuing regularization term was introduced on , which in a strict way reverts to choosing as the regularization term and solving the optimization problem Bruckstein et al., 2009. However, finding the optimal solution to the problem demands an exhaustive search across all possible combinations of the columns of . Hence, a pragmatic solution is to solve the convex-relaxed optimization problem for the -norm, commonly known as Basis Pursuit Denoising Chen et al., 2001 or equivalently as the least absolute shrinkage and selection operator (LASSO) Tibshirani, 1996:
which provides fast convergence to a global solution. Imposing sparsity on the activity-inducing signal implies that it is assumed to be well represented by a reduced subset of few non-zero coefficients at the fMRI timescale, which in turn trigger event-related BOLD responses. Hereinafter, this assumption is referred to as the spike model. However, even if PFM was developed as a spike model, its formulation in Eq. 6 can be extended to estimate the innovation signal, i.e., the derivative of the activity-inducing signal, as shown in Unifying Both Perspectives.
Total Activation¶
Alternatively, deconvolution can be formulated as if the signal to be recovered directly fits the measurements and at the same time satisfies some suitable regularization, which leads to
Under this analysis formulation, total variation (TV), i.e., the -norm of the derivative , is a powerful regularizer since it favors recovery of piecewise-constant signals Chambolle, 2004. Going beyond, the approach of generalized TV introduces an additional differential operator in the regularizer that can be tailored as the inverse operator of a linear system Karahanoglu et al., 2011, that is, . In the context of hemodynamic deconvolution, Total Activation is proposed for which the discrete operator is derived from the inverse of the continuous-domain linearized Balloon-Windkessel model Buxton et al., 1998Friston et al., 2000. The interested reader is referred to Khalidov et al., 2011Karahanoglu et al., 2011Karahanoğlu et al., 2013 for a detailed description of this derivation.
Therefore, the solution of the Total Activation (TA) problem
will yield the activity-related signal for which the activity-inducing signal and the so-called innovation signal , i.e., the derivate of the activity-inducing signal, will also be available, as they are required for the regularization. Modeling the activity-inducing signal based on the innovation signal is referred to as the block model. Nevertheless, even if TA was originally developed as a block model, its formulation in Eq. 8 can be made equivalent to the spike model as shown in Unifying Both Perspectives.
Unifying Both Perspectives¶
PFM and TA are based on the synthesis- and analysis-based formulation of the deconvolution problem, respectively. They are also tailored for the spike and block model, respectively. In the first case, the recovered deconvolved signal is synthesized to be matched to the measurements, while in the second case, the recovered signal is directly matched to the measurements but needs to satisfy its analysis in terms of deconvolution. This also corresponds to using the forward or backward model of the hemodynamic system, respectively. Hence, it is possible to make both approaches equivalent [Elad et al. (2007)][5].
To start with, TA can be made equivalent to PFM by adapting it for the spike model; i.e., when removing the derivative operator of the regularizer in Eq. 8, it can be readily verified that replacing in that case leads to identical equations and thus both assume a spike model, since and will cancel out each other [Karahanoglu et al. (2011)][6].
Conversely, the PFM spike model can also accommodate the TA block model by modifying [Eq.
activity-inducing signal is rewritten in terms of the innovation signal as where the matrix is the first-order integration operator Cherkaoui et al., 2019Uruñuela et al., 2020. This way, PFM can estimate the innovation signal as follows:
and becomes equivalent to TA by replacing , and thus adopting the block model. Based on the previous equations (Eq. 6), (Eq. 8) and ([Eq.
providing a convenient signal model according to the different assumptions of the underlying neuronal-related signal. This work evaluates the core of the two techniques; i.e., the regularized least-squares problem with temporal regularization without considering the spatial regularization term originally incorporated in TA. For the remainder of this paper, the PFM and TA formalisms with both spike and block models are used.
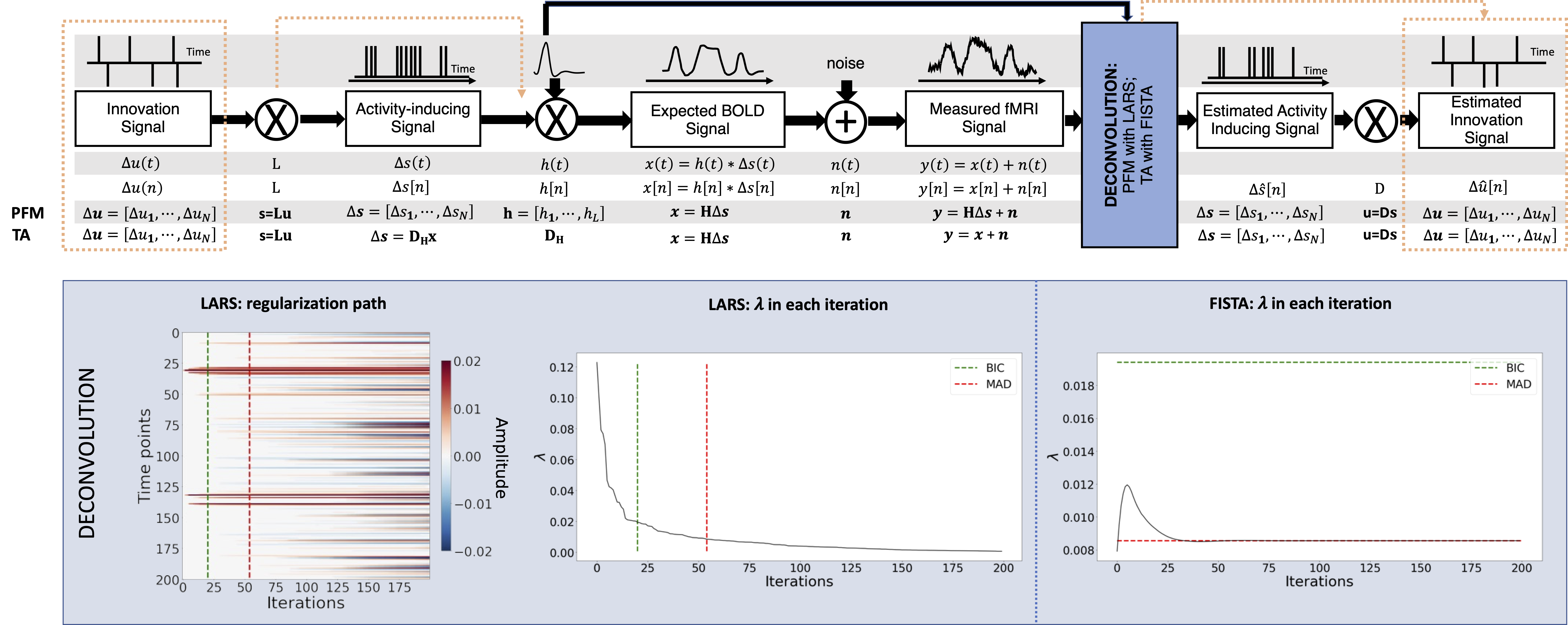
Figure 1:Flowchart detailing the different steps of the fMRI signal and the deconvolution methods described. The orange arrows indicate the flow to estimate the innovation signals, i.e., the derivative of the activity-inducing signal. The blue box depicts the iterative \textit{modus operandi} of the two algorithms used in this paper to solve the paradigm free mapping (PFM) and Total Activation (TA) deconvolution problems. The plot on the left shows the regularization path obtained with the least angle regression (LARS) algorithm, where the x-axis illustrates the different iterations of the algorithm, the y-axis represents points in time, and the color describes the amplitude of the estimated signal. The middle plot depicts the decreasing values of λ for each iteration of LARS as the regularization path is computed. The green and red dashed lines in both plots illustrate the Bayesian information criterion (BIC) and median absolute deviation (MAD) solutions, respectively. Comparatively, the changes in λ when the fast iterative shrinkage-thresholding algorithm (FISTA) method is made to converge to the MAD estimate of the noise are shown on the right. Likewise, the λ corresponding to the BIC and MAD solutions are shown with dashed lines.
Algorithms and Parameter Selection¶
Despite their apparent resemblance, the practical implementations of the PFM and TA methods proposed different algorithms to solve the corresponding optimization problem and select an adequate regularization parameter λ Gaudes et al., 2013Karahanoğlu et al., 2013. The PFM implementation available in AFNI employs the least angle regression (LARS) Efron et al., 2004, whereas the TA implementation uses the fast iterative shrinkage-thresholding algorithm (FISTA) Beck & Teboulle, 2009. The blue box in Figure 1 provides a descriptive view of the iterative \textit{modus operandi} of the two algorithms.
On the one hand, LARS is a homotopy approach that computes all the possible solutions to the optimization problem and their corresponding value of λ; i.e., the regularization path, and the solution according to the Bayesian Information Criterion (BIC) Schwarz, 1978, was recommended as the most appropriate in the case of PFM approaches since Akaike Information Criterion (AIC) often tends to overfit the signal Gaudes et al., 2013Caballero-Gaudes et al., 2019.
On the other hand, FISTA is an extension of the classical gradient algorithm that provides fast convergence for large-scale problems. In the case of FISTA though, the regularization parameter λ must be selected prior to solving the problem, but can be updated in every iteration so that the residuals of the data fit converge to an estimated noise level of the data :
where is the iteration estimate, and are the and iteration values for the regularization parameter λ, and is the number of points in the time-course. The pre-estimated noise level can be obtained as the median absolute deviation (MAD) of the fine-scale wavelet coefficients (Daubechies, order 3) of the fMRI timecourse. The MAD criterion has been adopted in TA Karahanoğlu et al., 2013. Of note, similar formulations based on the MAD estimate have also been applied in PFM formulations Gaudes et al., 2012Gaudes et al., 2011.
Methods¶
Simulated data¶
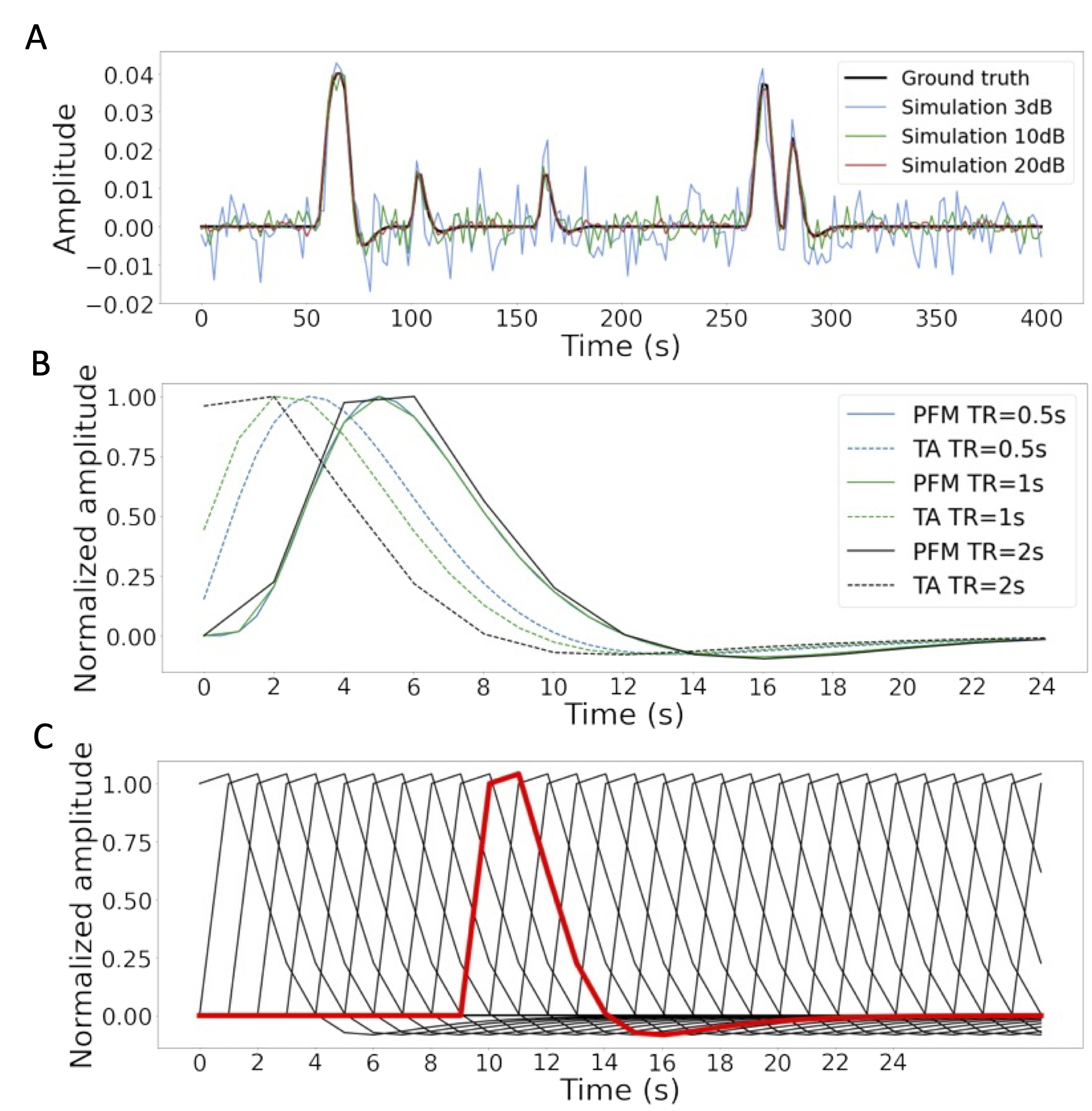
Figure 2:A) Simulated signal with different SNRs (20 dB, 10 dB and 3 dB) and ground truth given in signal percentage change (SPC). B) Canonical HRF models typically used by PFM (solid line) and TA (dashed line) at TR = 0.5 s (blue), TR = 1 s (green) and TR = 2 s (black). Without loss of generality, the waveforms are scaled to unit amplitude for visualization. C) Representation of shifted HRFs at TR = 2 s that build the design matrix for PFM when the HRF model has been matched to that in TA. The red line corresponds to one of the columns of the HRF matrix.
In order to compare the two methods while controlling for their correct performance, a simulation scenario was created, which can be found in the GitHub repository shared in Code and data availability. For the sake of illustration, here the simulations correspond to a timecourse with a duration of 400 seconds (TR = 2 s) where the activity-inducing signal includes 5 events, which are convolved with the canonical HRF. Different noise sources (physiological, thermal, and motion-related) were also added and three different scenarios with varying signal-to-noise ratios (SNR = 20, 10, 3 dB) were simulated, which represent high, medium and low contrast-to-noise ratios as shown in Figure 2A. Noise was created following the procedure in Gaudes et al., 2013 as the sum of uncorrelated Gaussian noise and sinusoidal signals to simulate a realistic noise model with thermal noise, cardiac and respiratory physiological fluctuations, respectively. The physiological signals were generated as
with up to second-order harmonics per cardiac ((f_{c,i})) and respiratory ((f_{r,i})) component that were randomly generated following normal distributions with variance 0.04 and mean (if_r) and (if_c), for (i = [1, 2]). The fundamental frequencies were set to (f_r = 0.3) Hz for the respiratory component Birn et al., 2006 and (f_c = 1.1) Hz for the cardiac component Shmueli et al., 2007. The phases of each harmonic (\phi) were randomly selected from a uniform distribution between 0 and 2π radians. To simulate physiological noise that is proportional to the change in BOLD signal, a variable ratio between the physiological ((\sigma_P)) and the thermal ((\sigma_0)) noise was modeled as (\sigma_P/\sigma_0 = a(tSNR)^b + c), where (a = 5.01 \times 10^{-6}), (b = 2.81), and (c = 0.397), following the experimental measures available in Table 3 from Triantafyllou et al., 2005).
Experimental Data¶
To compare the performance of the two approaches as well as illustrate their operation, two representative experimental datasets were employed.
Motor task dataset: One healthy subject was scanned in a 3T MR scanner (Siemens) under a Basque Center on Cognition, Brain and Language Review Board-approved protocol. T2*-weighted multi-echo fMRI data was acquired with a simultaneous-multislice multi-echo gradient echo-planar imaging sequence, kindly provided by the Center of Magnetic Resonance Research (University of Minnesota, USA) Feinberg et al., 2010Moeller et al., 2010Setsompop et al., 2011, with the following parameters: 340 time frames, 52 slices, Partial-Fourier = 6/8, voxel size = mm\textsuperscript{3}, TR = 1.5 s, TEs = 10.6/28.69/46.78/64.87/82.96 ms, flip angle = 70o, multiband factor = 4, GRAPPA = 2.
During the fMRI acquisition, the subject performed a motor task consisting of five different movements (left-hand finger tapping, right-hand finger tapping, moving the left toes, moving the right toes and moving the tongue) that were visually cued through a mirror located on the head coil. These conditions were randomly intermixed every 16 seconds, and were only repeated once the entire set of stimuli were presented. Data preprocessing consisted of first, discarding the first 10 volumes of the functional data to achieve a steady state of magnetization. Then, image realignment to the skull-stripped single-band reference image (SBRef) was computed on the first echo, and the estimated rigid-body spatial transformation was applied to all other echoes Jenkinson et al., 2012Jenkinson & Smith, 2001. A brain mask obtained from the SBRef volume was applied to all the echoes and the different echo timeseries were optimally combined (OC) voxelwise by weighting each timeseries contribution by its T2* value Posse et al., 1999. AFNI Cox, 1996 was employed for a detrending of up to 4\textsuperscript{th}-order Legendre polynomials, within-brain spatial smoothing (3 mm FWHM) and voxelwise signal normalization to percentage change. Finally, distortion field correction was performed on the OC volume with Topup Andersson et al., 2003, using the pair of spin-echo EPI images with reversed phase encoding acquired before the ME-EPI acquisition Glasser et al., 2016.
Resting-state datasets: One healthy subject was scanned in a 3T MR scanner (Siemens) under a Basque Center on Cognition, Brain and Language Review Board-approved protocol. Two runs of T2*-weighted fMRI data were acquired during resting-state, each with 10 min duration, with 1) a standard gradient-echo echo-planar imaging sequence (monoband) (TR = 2000 ms, TE = 29 ms, flip-angle = 78(^o), matrix size = , voxel size = mm3, 33 axial slices with interleaved acquisition, slice gap = 0.6 mm) and 2) a simultaneous-multislice gradient-echo echo-planar imaging sequence (multiband factor = 3, TR = 800 ms, TE = 29 ms, flip-angle = 60o, matrix size = , voxel size = mm3, 42 axial slices with interleaved acquisition, no slice gap). Single-band reference images were also collected in both resting-state acquisitions for head motion realignment. Field maps were also obtained to correct for field distortions.
During both acquisitions, participants were instructed to keep their eyes open, fixating a white cross that they saw through a mirror located on the head coil, and not to think about anything specific. The data was pre-processed using AFNI Cox, 1996. First, volumes corresponding to the initial 10 seconds were removed to allow for a steady-state magnetization. Then, the voxel time-series were despiked to reduce large-amplitude deviations and slice-time corrected. Inhomogeneities caused by magnetic susceptibility were corrected with FUGUE (FSL) using the field map images Jenkinson et al., 2012. Next, functional images were realigned to a base volume (monoband: volume with the lowest head motion; multiband: single-band reference image). Finally, a simultaneous nuisance regression step was performed comprising up to 6th-order Legendre polynomials, low-pass filtering with a cutoff frequency of 0.25 Hz (only on multiband data to match the frequency content of the monoband), 6 realignment parameters plus temporal derivatives, 5 principal components of white matter (WM), 5 principal components of lateral ventricle voxels (anatomical CompCor) Behzadi et al., 2007 and 5 principal components of the brain’s edge voxels Patriat et al., 2015. WM, cerebrospinal fluid (CSF) and brain’s edge-voxel masks were obtained from Freesurfer tissue and brain segmentations. In addition, scans with potential artifacts were identified and censored when the euclidean norm of the temporal derivative of the realignment parameters (ENORM) was larger than 0.4, and the proportion of voxels adjusted in the despiking step exceeded 10%.
Selection of the Hemodynamic Response Function¶
In their original formulations, PFM and TA specify the discrete-time HRF in different ways. For PFM, the continuous-domain specification of the canonical double-gamma HRF Henson & Friston, 2007 is sampled at the TR and then put as shifted impulse responses to build the matrix . In the case of TA, however, the continuous-domain linearized version of the balloon-windkessel model is discretized to build the linear differential operator in . While the TR only changes the resolution of the HRF shape for PFM, the impact of an equivalent impulse response of the discretized differential operator at different TR is more pronounced. As shown in Figure 2B, longer TR leads to equivalent impulse responses of TA that are shifted in time, provoking a lack of the initial baseline and rise of the response. The reader is referred to Figure S1 to see the differences in the estimation of the activity-inducing and innovation signals when both methods use the HRF in their original formulation. To avoid differences between PFM and TA based on their built-in HRF, the synthesis operator was built with shifted versions of the HRF given by the TA analysis operator (e.g., see Figure 2C for the TR=2s case).
Selection of the Regularization Parameter¶
The simulated data was used to compare the performance of the two deconvolution algorithms with both BIC and MAD criteria to set the regularization parameter λ (see Algorithms and Parameter Selection). Here, the evaluation also included investigating if the algorithms behave differently in terms of the estimation of the activity-inducing signal using the spike model described in Eq. 6 and the block model based on the innovation signal in Eq. 9.
For selection based on the BIC, LARS was initally performed with the PFM deconvolution model to obtain the solution for every possible λ in the regularization path. Then, the values of λ corresponding to the BIC optimum were adopted to solve the TA deconvolution model by means of FISTA.
For a selection based on the MAD estimate of the noise, the temporal regularization in its original form for TA was applied, whereas for PFM the selected λ corresponds to the solution whose residuals have the closest standard deviation to the estimated noise level of the data . %We do not introduce additional spatial regularization in any of the cases.
Analyses in Experimental fMRI Data¶
Difference between approaches: To assess the discrepancies between both approaches when applied on experimental fMRI data, the square root of the sum of squares of the differences (RSSD) between the activity-inducing signals estimated with PFM and TA were calculated on the three experimental datasets as
where is the number of timepoints of the acquisition. The RSSD of the innovation signals was computed equally.
Task fMRI data: In the analysis of the motor task data, the performance of PFM and TA was evaluated in comparison with a conventional General Linear Model analysis (3dDeconvolve in AFNI) that takes advantage of the information about the duration and onsets of the motor trials. Given the block design of the motor task, this comparison is only made with the block model.
Resting-state fMRI data: The usefulness of deconvolution approaches in the analysis of resting-state data where information about the timings of neuronal-related BOLD activity cannot be predicted is also illustrated. Apart from being able to explore individual maps of deconvolved activity (i.e., innovation signals, activity-inducing signals, or hemodynamic signals) at the temporal resolution of the acquisition (or deconvolution), here the average extreme points of the activity-inducing and innovation maps (given that these examples do not have a sufficient number of scans to perform a clustering step) is calculated to illustrate how popular approaches like co-activation patterns (CAPs) Tagliazucchi et al., 2012Liu et al., 2018 and innovation-driven co-activation patterns (iCAPs) Karahanoğlu & Van De Ville, 2015 can be applied on the deconvolved signals to reveal patterns of coordinated brain activity. To achieve this, the average time-series was calculated in a seed of 9 voxels located in the precuneus, supramarginal gyrus, and occipital gyri independently, and solve the deconvolution problem to find the activity-inducing and innovation signals in the seeds. Then, a 95th percentile threshold was applied and the maps of the time-frames that survive the threshold were averaged. Finally, the same procedure was applied to the original--- i.e., non-deconvolved--- signal in the seed and compare the results with the widely-used seed correlation approach.
Results¶
Performance Based on the Regularization Parameter¶
Figure 3A shows the regularization paths of PFM and TA side by side obtained for the spike model of Eq. 6 for SNR=3 dB. The solutions for all three SNR conditions are shown in Figure S2 and Figure S3. Starting from the maximum λ corresponding to a null estimate and for decreasing values of λ, LARS computes a new estimate at the value of λ that reduces the sparsity promoted by the -norm and causes a change in the active set of non-zero coefficients of the estimate (i.e., a zero coefficient becomes non-zero or vice versa) as shown in the horizontal axis of the heatmaps. Vertical dashed lines depict the selection of the regularization parameter based on the BIC, and thus, the colored coefficients indicated by these depict the estimated activity-inducing signal . Figure 3B illustrates the resulting estimates of the activity-inducing and activity-related hemodynamic signals when basing the selection of λ on the BIC for SNR=3 dB. Given that the regularization paths of both approaches are identical, it can be clearly observed that the BIC-based estimates are identical too for the corresponding λ. Thus, Figure 3A, Figure 3B, Figure S2 and Figure S3 demonstrate that, regardless of the simulated SNR condition, the spike model of both deconvolution algorithms produces identical regularization paths when the same HRF and regularization parameters are applied, and hence, identical estimates of the activity-inducing signal and neuronal-related hemodynamic signal .
Likewise, Figure 3C demonstrates that the regularization paths for the block model defined in Eq. 8 and Eq. 9 also yield virtually identical estimates of the innovation signals for both PFM and TA methods. Again, the BIC-based selection of λ is identical for both PFM and TA. As illustrated in Figure 3D, the estimates of the innovation signal also show no distinguishable differences between the algorithms. % Hence, Figure 3A-D demonstrate that both PFM and TA yield equivalent regularization paths and estimates of the innovation signal and activity-inducing signal regardless of the simulated SNR condition when applying the same HRF and regularization parameters with the block and spike models.
As for selecting λ with the MAD criterion defined in Eq. 10, Figure 3E depicts the estimated activity-inducing and activity-related signals for the simulated low-SNR setting using the spike model, while Figure 3F shows the estimated signals corresponding to the block model. Both plots in Figure 3E and F depict nearly identical results between PFM and TA with both models. Given that the regularization paths of both techniques are identical, minor dissimilarities are owing to the slight differences in the selection of λ due to the quantization of the values returned by LARS.
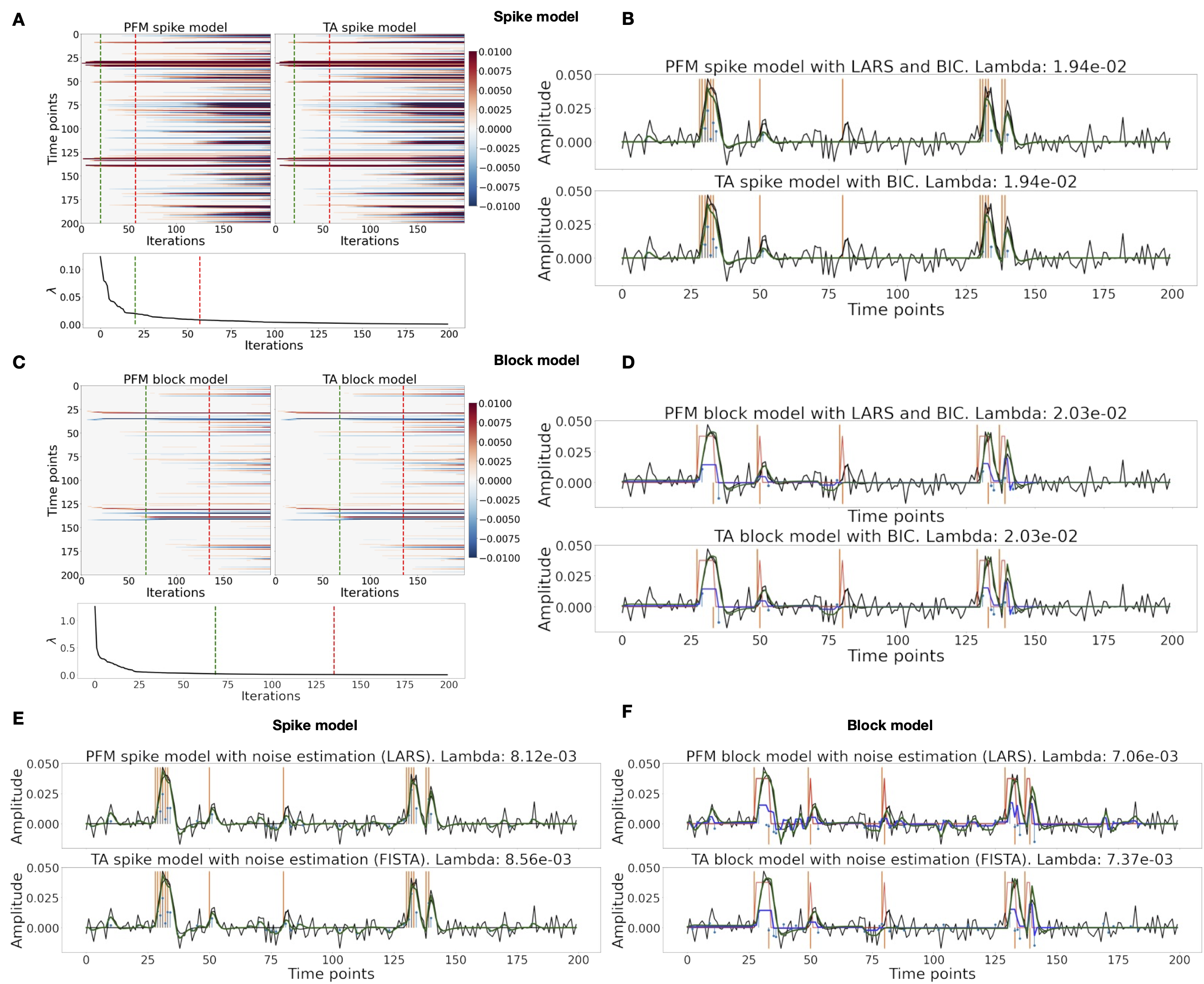
Figure 3:(A) Heatmap of the regularization paths of the activity-inducing signals (spike model) estimated with PFM and TA as a function of λ for the simulated data with SNR = 3 dB (x-axis: increasing number of iterations or λ as given by LARS; y-axis: time; color: amplitude). Vertical lines denote iterations corresponding to the BIC (dashed line) and MAD (dotted line) selection of λ. (B) Estimated activity-inducing (blue) and activity-related (green) signals with a selection of λ based on the BIC. Orange and red lines depict the ground truth. (C) Heatmap of the regularization paths of the innovation signals (block model) estimated with PFM and TA as a function of λ for the simulated data with SNR = 3 dB. (D) Estimated innovation (blue), activity-inducing (darker blue), and activity-related (green) signals with a selection of λ based on the BIC. (E) Activity-inducing and activity-related (fit, ) signals estimated with PFM (top) and TA (bottom) when λ is selected based on the MAD method with the spike model, and (F) with the block model for the simulated data with SNR = 3 dB.
Performance on Experimental Data¶
Figure 4 depicts the RSSD maps revealing differences between PFM and TA estimates for the spike (Figure 4A and C) and block (Figure 4B and D) models when applied to the three experimental fMRI datasets. The RSSD values are virtually negligible (i.e., depicted in yellow) in most of the within-brain voxels and lower than the amplitude of the estimates of the activity-inducing and innovation signals. Based on the maximum value of the range shown in each image, it can be observed that the similarity between both approaches is more evident for the spike model (with both selection criteria) and the block model with the BIC selection. However, given the different approaches used for the selection of the regularization parameter λ based on the MAD estimate of the noise (i.e., converging so that the residuals of FISTA are equal to the MAD estimate of the noise for TA vs. finding the LARS residual that is closest to the MAD estimate of the noise), higher RSSD values can be observed with the largest differences occurring in gray matter voxels. These areas also correspond to low values of λ (see Figure S4) and MAD estimates of the noise (see Figure S5), while the highest values are visible in regions with signal droupouts, ventricles, and white matter. These differences that arise from the different approaches to find the optimal regularization parameter based on the MAD estimate of the noise can be clearly seen in the root sum of squares (RSS) of the estimates (Figure S6). These differences are also observable in the ATS calculated from estimates obtained with the MAD selection as shown in Figure S9. However, the identical regularization paths shown in Figure S7 demonstrate that both methods perform equivalently on experimental data (see estimates of innovation signal obtained with an identical selection of λ in Figure S8). Hence, the higher RSSD values originate from the different methods to find the optimal regularization parameter based on the MAD estimate of the noise that yield different solutions as shown by the dashed vertical lines in Figure S7.
Figure 4:Square root of the sum of squared differences (RSSD) between the estimates obtained with PFM and TA for (A) spike model (activity-inducing signal) and BIC selection of λ, (B) block model (innovation signal) and BIC selection, (C) spike model (activity-inducing signal) and MAD selection, (D) block model (innovation signal) and MAD selection. RSSD maps are shown for the three experimental fMRI datasets: the motor task (Motor), the monoband resting-state (Mono), and the multiband resting-state (Multi) datasets.
Figure 5 depicts the results of the analysis of the Motor dataset with the PFM and TA algorithms using the BIC selection of λ (see Figure S9 for results with MAD selection), as well as a conventional GLM approach. The Activation Time Series (top left), calculated as the sum of squares of all voxel amplitudes (positive vs. negative) for a given moment in time, obtained with PFM and TA show nearly identical patterns. These ATS help to summarize the four dimensional information available in the results across the spatial domain and identify instances of significant BOLD activity. The second to sixth rows show the voxel timeseries and the corresponding activity-related, activity-inducing and innovation signals obtained with PFM using the BIC criterion of representative voxels in the regions activated in each of the motor tasks. The TA-estimated time-series are not shown because they were virtually identical. The maps shown on the right correspond to statistical parametric maps obtained with the GLM for each motor condition () as well as the maps of the PFM and TA estimates at the onsets of individual motor events (indicated with arrows in the timecourses). The estimated activity-related, activity-inducing and innovation signals clearly reveal the activity patterns of each condition in the task, as they exhibit a BOLD response locked to the onset and duration of the conditions. Overall, activity maps of the innovation signal obtained with PFM and TA highly resemble those obtained with a GLM for individual events, with small differences arising from the distinct specificity of the GLM and deconvolution analyses. Notice that the differences observed with the different approaches to select λ based on the MAD estimate shown in Figure 4 are reflected on the ATS shown in Figure S9 as well.
Figure 5:Activity maps of the motor task using a selection of λ based on the BIC estimate. Row 1: Activation time-series (ATS) of the innovation signals estimated by PFM (in blue) or TA (in red) calculated as the sum of squares of all voxels at every timepoint. Positive-valued and negative-valued contributions were separated into two distinct time-courses. Color-bands indicate the onset and duration of each condition in the task (green: tongue motion, purple: left-hand finger-tapping, blue: right-hand finger-tapping, red: left-foot toes motion, orange: right-foot toes motion). Rows 2-6: time-series of a representative voxel for each task with the PFM-estimated innovation (blue), PFM-estimated activity-inducing (green), and activity-related (i.e., fitted, orange) signals, with their corresponding GLM, PFM, and TA maps on the right (representative voxels indicated with green arrows). Amplitudes are given in signal percentage change (SPC). The maps shown on the right are sampled at the time-points labeled with the red arrows and display the innovation signals at these moments across the whole brain.
As an illustration of the insights that deconvolution methods can provide in the analysis of resting-state data, Figure 6 depicts the average activity-inducing and innovation maps of common resting-state networks obtained from thresholding and averaging the activity-inducing and innovation signals, respectively, estimated from the resting-state multiband data using PFM with a selection of λ based on the BIC. The average activity-inducing maps obtained via deconvolution show spatial patterns of the default mode network (DMN), dorsal attention network (DAN), and visual network (VIS) that highly resemble the maps obtained with conventional seed correlation analysis using Pearson’s correlation, and the average maps of extreme points of the signal (i.e., with no deconvolution). With deconvolution, the average activity-inducing maps seem to depict more accurate spatial delineation (i.e., less smoothness) than those obtained from the original data, while maintaining the structure of the networks. The BIC-informed selection of λ yields spatial patterns of average activity-inducing and innovation maps that are more sparse than those obtained with a selection of λ based on the MAD estimate (see Figure S10). Furthermore, the spatial patterns of the average innovation maps based on the innovation signals using the block model yield complementary information to those obtained with the activity-inducing signal since iCAPs allow to reveal regions with synchronous innovations, i.e., with the same upregulating and downregulating events. For instance, it is interesting to observe that the structure of the visual network nearly disappears in its corresponding average innovation maps, suggesting the existence of different temporal neuronal patterns across voxels in the primary and secondary visual cortices.
Figure 6:Average activity-inducing (left) and innovation (right) maps obtained from PFM-estimated activity-inducing and innovation signals, respectively, using a BIC-based selection of λ. Time-points selected with a 95\textsuperscript{th} percentile threshold (horizontal lines) are shown over the average time-series (blue) in the seed region (white cross) and the deconvolved signals, i.e., activity inducing (left) and innovation (right) signals (orange). Average maps of extreme points and seed correlation maps are illustrated in the center.
Discussion and Conclusion¶
Hemodynamic deconvolution can be formulated using a synthesis- and analysis-based approach as proposed by PFM and TA, respectively. This work demonstrates that the theoretical equivalence of both approaches is confirmed in practice given virtually identical results when the same HRF model and equivalent regularization parameters are employed. Hence, it can be argued that previously observed differences in performance can be explained by specific settings, such as the HRF model and selection of the regularization parameter (as shown in Figure 4, Figure S6 and Figure S7), convergence thresholds, as well as the addition of a spatial regularization term in the spatiotemporal TA formulation Karahanoğlu et al., 2013. For instance, the use of PFM with the spike model in Tan et al. (2017) was seen not to be adequate due to the prolonged trials in the paradigm, which better fit the block model as described in Eq. 9. However, given the equivalence of the temporal deconvolution, incorporating extra spatial or temporal regularization terms in the optimization problem should not modify this equivalence providing convex operators are employed. For a convex optimization problem, with a unique global solution, iterative shrinkage thresholding procedures alternating between the different regularization terms guarantee convergence, such as the generalized forward-backward splitting Raguet et al., 2013 algorithm originally employed for TA.
Our findings are also in line with the equivalence of analysis and synthesis methods in under-determined cases () demonstrated in Elad et al., 2007 and Ortelli & Geer, 2019. Still, this chapter has shown that a slight difference in the selection of the regularization parameter can lead to small differences in the estimated signals when employing the block model with the BIC selection of λ. However, since their regularization paths are equivalent, the algorithms can easily be forced to converge to the same selection of λ, thus resulting in identical estimated signals.
Nevertheless, the different formulations of analysis and synthesis deconvolution models bring along different kinds of flexibility. One notable advantage of PFM is that it can readily incorporate any HRF as part of the synthesis operator Elad et al., 2007, only requiring the sampled HRF at the desired temporal resolution, which is typically equal to the TR of the acquisition. Conversely, TA relies upon the specification of the discrete differential operator that inverts the HRF, which needs to be derived either by the inverse solution of the sampled HRF impulse response, or by discretizing a continuous-domain differential operator motivated by a biophysical model. The more versatile structure of PFM allows for instance an elegant extension of the algorithm to multi-echo fMRI data Caballero-Gaudes et al., 2019 where multiple measurements relate to a common underlying signal. Therefore, the one-to-many synthesis scenario (i.e., from activity-inducing to several activity-related signals) is more cumbersome to express using TA. In other words, a set of differential operators should be defined and the differences between their outputs constrained. In contrast, the one-to-many analysis scenario (i.e., from the measurements to several regularizing signals) is more convenient to be expressed by TA, for example combining spike and block regularizers. While the specification of the differential operator in TA only indirectly controls the HRF, the use of the derivative operator to enforce the block model, instead of the integrator in PFM, impacts positively the stability and rate of the convergence of the optimization algorithms. Moreover, analysis formulations can be more suitable for online applications that are still to be explored in fMRI data, but are employed for calcium imaging deconvolution Friedrich et al., 2017Jewell et al., 2019, and which have been applied for offline calcium deconvolution Farouj et al., 2020.
Moreover, deconvolution techniques can be used before more downstream analysis of brain activity in terms of functional network organization as they estimate interactions between voxels or brain regions that occur at the activity-inducing level, and are thus less affected by the slowness of the hemodynamic response compared to when the BOLD signals are analyzed directly. In particular, hemodynamic deconvolution approaches hold a close parallelism to recent methodologies aiming to understand the dynamics of neuronal activations and interactions at short temporal resolution and that focus on extreme events of the fMRI signal. As an illustration, Figure 6 shows that the innovation- or activity-inducing CAPs computed from deconvolved events in a single resting-state fMRI dataset closely resemble the conventional CAPs computed directly from extreme events of the fMRI signal Liu & Duyn, 2013Liu et al., 2013Liu et al., 2018Cifre et al., 2020Cifre et al., 2020Zhang et al., 2020Tagliazucchi et al., 2011Tagliazucchi et al., 2012Tagliazucchi et al., 2016Rolls et al., 2021. Similarly, it can be hypothesized that these extreme events will also show a close resemblance to intrinsic ignition events Deco & Kringelbach, 2017Deco et al., 2017. As shown in the maps, deconvolution approaches can offer a more straightforward interpretability of the activation events and resulting functional connectivity patterns. Here, CAPs were computed as the average of spatial maps corresponding to the events of a single dataset. Beyond simple averaging, clustering algorithms (e.g., K-means and consensus clustering) can be employed to discern multiple CAPs or iCAPs at the whole-brain level for a large number of subjects. Previous findings based on iCAPs have for instance revealed organizational principles of brain function during rest Karahanoğlu & Van De Ville, 2015 and sleep Tarun et al., 2021 in healthy controls, next to alterations in 22q11ds Zoeller et al., 2019 and multiple sclerosis Bommarito et al., 2021.
Next to CAPs-inspired approaches, dynamic functional connectivity has recently been investigated with the use of co-fluctuations and edge-centric techniques Faskowitz et al., 2020Esfahlani et al., 2020Jo et al., 2021Sporns et al., 2021Oort et al., 2018. The activation time series shown in Figure 5A aims to provide equivalent information to the root of sum of squares timecourses used in edge-centric approaches, where timecourses with peaks delineate instances of significant brain activity. Future work could address which type of information is redundant or distinct across these frameworks. These examples illustrate that deconvolution techniques can be employed prior to other computational approaches and could serve as an effective way of denoising the fMRI data. Hence, an increase in the number of studies that take advantage of the potential benefits of using deconvolution methods prior to functional connectivity analyses can be expected.
Even though the two approaches examined here provide alternative representations of the BOLD signals in terms of innovation and activity-inducing signals, their current implementations have certain limitations and call for further developments or more elaborate models, where some of them have been partially addressed in the literature. One relevant focus is to account for the variability in HRF that can be observed in different regions of the brain. First, variability in the temporal characteristics of the HRF can arise from differences in stimulus intensity and patterns, as well as with short inter-event intervals like in fast cognitive processes or experimental designs Yeşilyurt et al., 2008Sadaghiani et al., 2009Chen et al., 2021Polimeni & Lewis, 2021. Similarly, the HRF shape at rest might differ from the canonical HRF commonly used for task-based fMRI data analysis. A wide variety of HRF patterns could be elicited across the whole brain and possible detected with sufficiently large signal-to-noise ratio. For instance, Gonzalez-Castillo et al. (2012) showed two gamma-shaped responses at the onset and the end of the evoked trial, respectively. This unique HRF shape would be deconvolved as two separate events with the conventional deconvolution techniques. The impact of HRF variability could be reduced using structured regularization terms along with multiple basis functions Gaudes et al., 2012 or procedures that estimate the HRF shape in an adaptive fashion in both analysis Farouj et al., 2019 and synthesis formulations Cherkaoui et al., 2021.
Another avenue of research consists in leveraging spatial information by adopting multivariate deconvolution approaches that operate at the whole-brain level, instead of working voxelwise and beyond regional regularization terms (e.g., as proposed in Karahanoğlu et al. (2013)). Operating at the whole-brain level would open the way for methods that consider shared neuronal activity using mixed norm regularization terms Uruñuela-Tremiño et al., 2019, as described in Chapter 4: Whole-Brain Multivariate Deconvolution for Multi-Echo Functional MRI, or can capture long-range neuronal cofluctuations using low rank decompositions Cherkaoui et al., 2021. For example, multivariate deconvolution approaches could yield better localized activity patterns while reducing the effect of global fluctuations such as respiratory artifacts, which cannot be modelled at the voxel level with a multivariate sparse and low-rank model Uruñuela et al., 2021, as described in Chapter 6: Sparse and Low-Rank Paradigm Free Mapping.
Similar to solving other inverse problems by means of regularized estimators, the selection of the regularization parameter is critical to correctly estimate the neuronal-related signal. Hence, methods that take advantage of a more robust selection of the regularization parameter could considerably yield more reliable estimates of the neuronal-related signal. For instance, the stability selection procedure [Meinshausen & Bühlmann (2010);Urunuela2020StabilityBasedSparse] could be included to the deconvolution problem to ensure that the estimated coefficients are obtained with high probability. This approach is described in Chapter 3: Stability-Based Sparse Paradigm Free Mapping Uruñuela et al., 2020. Furthermore, an important issue of regularized estimation is that the estimates are biased with respect to the true value. In that sense, the use of non-convex -norm regularization terms (e.g., ) can reduce this bias while maintaining the sparsity constraint, at the cost of potentially converging to a local minima of the regularized estimation problem. In practice, these approaches could avoid the optional debiasing step that overcomes the shrinkage of the estimates and obtain a more accurate and less biased fit of the fMRI signal Gaudes et al., 2013Caballero-Gaudes et al., 2019. Finally, cutting-edge developments on physics-informed deep learning techniques for inverse problems Akçakaya et al., 2021Monga et al., 2021Ongie et al., 2020Cherkaoui et al., 2020 could be transferred for deconvolution by considering the biophysical model of the hemodynamic system and could potentially offer algorithms with reduced computational time and more flexibility.
Code and data availability¶
The code and materials used in this work can be found in the following GitHub repository:
https://
- Uruñuela, E., Bolton, T. A. W., Van De Ville, D., & Caballero-Gaudes, C. (2023). Hemodynamic Deconvolution Demystified: Sparsity-Driven Regularization at Work. Aperture Neuro, 3, 1–25. 10.52294/001c.87574
- Ogawa, S., Lee, T. M., Kay, A. R., & Tank, D. W. (1990). Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proceedings of the National Academy of Sciences, 87(24), 9868–9872. 10.1073/pnas.87.24.9868
- Logothetis, N. K., Pauls, J., Augath, M., Trinath, T., & Oeltermann, A. (2001). Neurophysiological investigation of the basis of the fMRI signal. Nature, 412(6843), 150–157. 10.1038/35084005
- Boynton, G. M., Engel, S. A., Glover, G. H., & Heeger, D. J. (1996). Linear Systems Analysis of Functional Magnetic Resonance Imaging in Human V1. The Journal of Neuroscience, 16(13), 4207–4221. 10.1523/jneurosci.16-13-04207.1996
- Cohen, M. S. (1997). Parametric Analysis of fMRI Data Using Linear Systems Methods. NeuroImage, 6(2), 93–103. 10.1006/nimg.1997.0278