This chapter was published as Uruñuela et al. (2024).
This chapter proposes a novel hemodynamic deconvolution algorithm, multivariate sparse paradigm
free mapping (Mv-SPFM), that operates at the whole brain level and adds spatial information via a
mixed-norm regularization term over all voxels. Additionally, Mv-SPFM employs the stability
selection procedure that removes the need to select regularization parameters and also lets us
obtain an estimate of the true probability of having a neuronal-related BOLD event at each voxel
and time-point based on the area under the curve (AUC) of the stability paths. Besides, its
formulation is adapted for multi-echo fMRI acquisitions (MvME-SPFM), which allows us to better
isolate fluctuations of BOLD origin on the basis of their linear dependence with the echo time (TE)
and to assign physiologically interpretable units (i.e., changes in the apparent transverse
relaxation ) to the resulting deconvolved events. Remarkably, Mv-SPFM also achieves
comparable performance when using a conventional single-echo formulation. The MV-SPFM algorithm
outperforms previous hemodynamic deconvolution approaches, showing higher spatial and temporal
agreement with the activation maps and BOLD signals obtained with a standard model-based linear
regression approach. Furthermore, owing to the stability selection, the proposed algorithm provides
more reliable estimates of neuronal-related activity for the study of the dynamics of brain
activity when no information about the timings of the BOLD events is available. This algorithm is
publicly available as part of the splora Python package at
https://
Introduction¶
Conventionally, the analysis of functional MRI (fMRI) data relies on available information about the experimental paradigm to establish hypothesized models of brain activity. However, this information can be inaccurate, incomplete or unavailable in multiple scenarios such as resting-state, naturalistic paradigms or clinical conditions. In these cases, blind estimates of neuronal-related activity can be obtained with paradigm-free analysis methods such as hemodynamic deconvolution. Yet, current formulations of the hemodynamic deconvolution problem have three important limitations: 1) their efficacy strongly depends on the appropriate selection of regularization parameters, 2) being univariate, they do not take advantage of the information present across the brain, and 3) they do not provide any measure of statistical certainty associated with each detected event.
Wouldn’t it be nice to have a probability of having an event at each time-point and for each voxel? Despite the range of deconvolution methods that have been developed, few capitalize on the various properties of fMRI data, such as the advantages of multi-echo fMRI for denoising fMRI data Bright & Murphy, 2013Kundu et al., 2017, or the use of tissue-based or parcellation-based information to improve the accuracy of the estimates of neuronal activity. Recent exceptions include deconvolution algorithms that incorporate a multivariate formulation to perform spatio-temporal deconvolution Bolton et al., 2019Uruñuela et al., 2021Costantini et al., 2022Cherkaoui et al., 2021, thus addressing the second limitation stated in the previous paragraph. In addition, one deconvolution algorithm has been presented that exploits the mono-exponential decay model of the multi-echo fMRI signal: multi-echo sparse Paradigm Free Mapping (ME-SPFM) Caballero-Gaudes et al., 2019. Furthermore, approaches have been developed to deal with the third limitation stated above and estimate the likelihood of having a neuronal event at each time-point and for each voxel by means of logistic regression Bush & Cisler, 2013Bush et al., 2015 or Gaussian mixture models Pidnebesna et al., 2019. However, wouldn’t it be desirable to have an algorithm that addresses all three limitations mentioned above? Specifically, it would be beneficial to obtain a measure of the probability of each voxel containing a neuronal event at each time-point using regularized estimators, while also leveraging the spatio-temporal information and physical properties of the fMRI signal for estimating the activity-inducing signal.
This chapter proposes a novel approach for the hemodynamic deconvolution of fMRI data that operates at the whole-brain level (i.e., multivariate formulation) to incorporate spatial information through a mixed-norm regularization term. Furthermore, this work proposes a stability selection procedure Meinshausen & Bühlmann, 2010 that makes the estimation of the neuronal activity more robust to the selection of the regularization parameters, while providing the likelihood of having a neuronal-related event at each time-point and for each voxel. Using multi-echo fMRI data acquired from 10 healthy subjects (16 datasets) this chapter demonstrates that the proposed multivariate multi-echo Paradigm Free Mapping (MvME-SPFM) algorithm not only provides more robust estimates of the neuronal activity, but also yields a measure of the probability of each voxel containing a neuronal event at each time-point. Moreover, MvME-SPFM returns quantitative estimates of in interpretable units (s-1), which is relevant for functional analysis across different acquisition methods and field strengths. The chapter is structured as follows: the multivariate signal model and the multivariate multi-echo PFM algorithm are introduced in Theory; Methods describes the data used and the analysis performed to evaluate this novel algorithm; the results of applying this new algorithm on experimental fMRI data are presented and compared to the previous PFM algorithms in Results; finally, the findings are discussed in Discussion and Conclusion.
Theory¶
Signal Model for Whole-Brain Deconvolution¶
Chapter 2: Synthesis-Based and Analysis-Based Hemodynamic Deconvolution for fMRI introduced that the BOLD fMRI signal model of a particular voxel can be written in matrix notation as:
where, assuming zero-boundary conditions, the variables , , are the voxel’s time-series, the activity-inducing signal changes and the noise term, respectively, and is the Toeplitz convolution matrix defined by the HRF Gitelman et al., 2003Gaudes et al., 2013. Hereinafter in the chapter, the noise term is assumed to be an additive white Gaussian noise (i.e., uncorrelated). Furthermore, the can be defined in a finer temporal resolution (i.e., increasing its dimension by a factor such that ) so that it can describe activity-inducing signal changes that are asynchronous to the TR of the data. Though in such scenario, the convolution matrix becomes non-Toeplitz (i.e. ) Ciuciu et al., 2003.
The previous signal model is applicable for single-echo and multi-echo fMRI data. In the particular case of multi-echo fMRI acquired with a gradient-echo sequence, the voxel’s time-series in terms of the signal percentage change has a linear relationship with the echo time (TE) as , where denotes the BOLD-like signal changes and corresponds to changes in the net magnetization, for instance due to head motion Kundu et al., 2017. The signal changes associated to fluctuations in the net magnetization can be effectively reduced in preprocessing, for example using multi-echo independent component analysis Kundu et al., 2012Caballero-Gaudes et al., 2019, and are neglected hereinafter. Hence, considering that neuronal-related signal changes produce a change in , the signal model in Eq. 1 can be adapted to contain the signal acquired at all echo-times (TE) via concatenation:
which can be simplified into , where , and .
Assuming that the shape of the hemodynamic response can be similarly modeled across all brain voxels, the previous voxel-wise (i.e., univariate) model in Eq. 2 can be extended straightforwardly to a multivariate formulation that considers all the voxels of the brain:
which can be simplified into , where , and .
Solving the Optimization Problem for Whole-Brain Deconvolution¶
As described in Chapter 2: Synthesis-Based and Analysis-Based Hemodynamic Deconvolution for fMRI, an estimate of the activity that induces the BOLD response can be obtained by solving an ordinary least-squares problem such as:
where λ is the regularization parameter that regulates the level of sparsity of the estimates given the -norm, which is defined as .
The inverse problem in Eq. 4 can be directly adapted to be solved at the whole-brain using the multivariate formulation in Eq. 3. More interestingly though, solving the inverse problem at the whole-brain level opens up many possibilities in the form of additional regularization terms to take advantage of the spatial information for an informed estimation of the activity-inducing signal . For instance, mixed-norms in the form of can be employed to separate coefficients into groups that are blind to each other, while the coefficients within a group are treated together Kowalski, 2009. Hence, regularization terms based on mixed-norms can promote spatio-temporal structures that are observed in fMRI signals.
Here, an mixed-norm regularization term Gramfort et al., 2011 is added to the multivariate convex problem to promote the co-activation of the activity-inducing signal considering the coefficients of the voxels of the brain () at time as one group:
where -norm is defined as , and is a parameter that controls the tradeoff between the sparsity introduced by the -norm and the grouping of voxels promoted by the -norm so that the estimation of one voxel coefficient at time is influenced by the estimates of the rest of the brain voxels at the same time. Note that when Eq. 5 is the whole-brain equivalent of Eq. 4. Additionally, it is worth noting that mixed-norm regularization, such as group LASSO, has been previously used in MEG/EEG studies Gramfort et al., 2011. However, in those cases, the spatial and temporal dimensions were swapped compared to Eq. 5.On the other hand, the regularization parameter λ can be adapted voxel-wise in order to account for differences in the signal-to-noise ratio across voxels. Consequently, the multivariate deconvolution problem can be written as:
where is a diagonal matrix with the voxel-specific values of λ. In practice, a criterion must be used to select the voxel-specific λs. Instead, the use of stability selection to avoid this critical choice is proposed (see Stability Selection of the Regularization Parameter λ).
Therefore, given the convex nature of the inverse problem in Eq. %s, estimates of can be calculated using the fast iterative shrinkage-thresholding algorithm (FISTA) Beck & Teboulle, 2009 with the following proximity operator for :
where , for , and by convention.
Methods¶
fMRI Data Acquisition and Preprocessing¶
The evaluation of the proposed MvME-SPFM was performed on ME-fMRI data acquired in 10 subjects using a multi-task rapid event-related paradigm. Six subjects performed two functional runs, the other 4 subjects only performed 1 run due to scanning time constraints (i.e., a total of 16 datasets). All participants gave informed consent in compliance with the NIH Combined Neuroscience International Review Board-approved protocol 93-M-1070 in Bethesda, MD. A thorough description of the MRI acquisition protocols and experimental tasks in the experimental design can be found in Gonzalez-Castillo et al., 2016, only those details that are relevant to this analysis are given here.
MRI data was acquired on a General Electric 3T 750 MRI scanner with a 32-channel receive-only head coil (General Electric, Waukesha, WI). Functional scans were acquired with a ME gradient-recalled echoplanar imaging (GRE-EPI) sequence (flip angle = for 9 subjects, flip angle = for 1 subject, TEs = 16.3/32.2/48.1 ms, TR = 2 s, 30 axial slices, slice thickness = 4 mm, in-plane resolution = mm2, FOV 192 mm, acceleration factor 2, number of acquisitions = 220). Functional data was acquired with ascending sequential slice acquisitions, except in one subject where the acquisitions were interleaved. In addition, high resolution T1-weighted MPRAGE and proton density images were acquired per subject for anatomical alignment and visualization purposes (176 axial slices, voxel size = mm3, image matrix = ).
Each run of data acquisition consisted of 6 trials with 5 different tasks each: biological motion observation (BMOT), finger tapping (FTAP), passive viewing of houses (HOUS), listening to music (MUSI), and sentence reading (READ). The reader is referred to that paper for details on the preprocessing steps, and comparison with alternative single-echo models for deconvolution. This data had previously been employed, preprocessed and ME-ICA denoised for the evaluation of the ME-SPFM algorithm in Caballero-Gaudes et al., 2019.
Stability Selection of the Regularization Parameter λ¶
The choice of the regularization parameter λ is crucial to obtain accurate estimates of . Although the value of λ of each voxel could be fixed ad-hoc, previous work has opted for the use of model selection criteria, such as the Bayesian Information Criterion (BIC), on the regularization path Caballero-Gaudes et al., 2019, computed by means of the least angle regression (LARS) algorithm Efron et al., 2004. Even though the use of BIC performed well for ME-SPFM Caballero-Gaudes et al., 2019 and its single-echo counterpart (SPFM) Gaudes et al., 2013, due to its high specificity, it can be problematic for certain voxels where the BIC curve might present multiple local minima or even fail to present a clear minima for the evaluated range of λ.
This chapter proposes a more robust procedure to address this shortcoming for selecting λ with the usage of the stability selection method Meinshausen & Bühlmann, 2010 described in Chapter 3: Stability-Based Sparse Paradigm Free Mapping. Moreover, the stability selection procedure presented here yields the probability to have a non-zero coefficient in the activity-inducing signal at each time-point. Specifically, our implementation of the stability selection procedure generates surrogates of each voxel timecourse by randomly subsampling 60% of the time-points (a more computationally expensive version was also tested with surrogates that yielded very similar results). The convolution matrix is subsampled accordingly. The surrogate data is then analyzed with the inverse problem in Eq. 5 for a voxel-specific range of λ values using the fast iterative shrinkage thresholding algorithm (FISTA). Here, 30 values of λ are spaced logarithmically between 5% and 95% of the voxel-specific maximum λ possible to more accurately sample the lower range. Then, the ratio (probability) of surrogates where the estimated coefficient at each time-point is non-zero is calculated for each time-point and value of λ. As illustrated in Figure 1, these probabilities build the so-called stability paths, which resemble the well-known regularization paths of conventional regularized estimators (e.g., LASSO, Ridge Regression) that plot the amplitude of the coefficients for each λ.
Unlike the original stability selection procedure, which sets a given probability threshold to select the final set of non-zero coefficients Meinshausen & Bühlmann, 2010, the area under the curve (AUC) of the stability path of each time-point is calculated as an index of confidence of having a non-zero coefficient across the evaluated range of λ. As a result, the AUC timecourse provides a measure of the probability of having neuronal-related activity at each time-point and voxel. Next, the AUC time-series are thresholded according to the histogram of AUC values in a region of non-interest (hereinafter, denoted as the null AUC histogram) to yield a sparse representation of the signal. Alternatively, a null distribution of AUC values could be generated from surrogate data Liégeois et al., 2021. Accordingly, when employing stability selection, the individual voxels’ estimates might not be equivalent to the voxels’ estimates in any single one of the whole-brain models that can be formulated with a given value of λ in Eq. 5 or in Eq. 6), but are rather obtained by computing area-under-the-curve (AUC) values for neuronal-related events.
Finally, a fitting step is applied to each voxel by defining a reduced convolution model with the selected non-zero coefficients and fitting it by means of a conventional orthogonal least squares estimator. This step reduces the bias towards zero imposed by the sparsity-promoting regularization terms, and thus obtains more realistic estimates of the neuronal-related signal (here, in terms of ) Caballero-Gaudes et al., 2019.
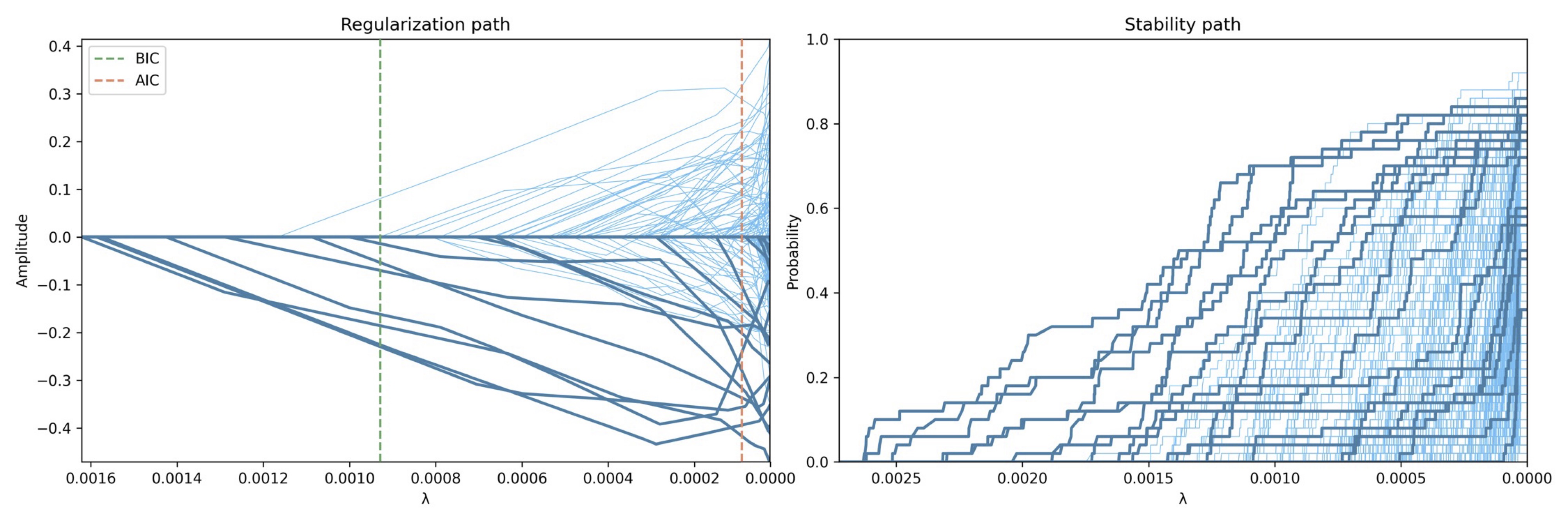
Figure 1:Example of the regularization path and the stability path for a voxel timeseries with . On the left, the regularization path shows the amplitude of each coefficient estimate (one per TR). At first, all the coefficients are zero and successively they become non-zero as λ decreases towards zero, which corresponds to the orthogonal least squares solution (i.e., no regularization). On the right, the corresponding stability path plots the probablity that each coefficient estimate (i.e., each TR) is non-zero for each value of λ based on the stability selection procedure. Note that both paths can have a different maximum value of λ given the subsampling step in the stability selection. Lines in the stability path correspond to different TRs of a single voxel. The darker lines denote the coefficient estimates corresponding to the TRs during the task-related events.
Balancing the Spatial Regularization¶
The -norm regularization term in Eq. 5 promotes structured spatio-temporal sparsity in the sense that the estimates of all brain voxels at a given time-point are treated as a group and this term forms a constraint on the number of groups with at least one non-zero estimate to model the data. Assuming that , either the value of all the voxel estimates at one time point can be non-zero or all of them are nulled. Hence, this regularization term considers spatial information from all brain voxels for the deconvolution since the value of a given voxel coefficient also depends on the rest of the voxels.
To illustrate the effect of the corresponding regularization parameter ρ, this chapter solves the multivariate regularization problem in Eq. 5 using stability selection for , and .; i.e., applying the sparsity-promoting -norm only, equally weighting the sparsity and spatial regularizations, and employing the -norm spatial regularization only, respectively.
Comparison with Conventional Timing-Based GLM Analyses¶
To evaluate how the multivariate formulation combined with stability selection improves the accuracy of the estimates of compared with its univariate counterpart ME-SPFM using the BIC for voxel-wise selection of λ Caballero-Gaudes et al., 2019, the spatial sensitivity, specificity and overlap (using a Dice coefficient metric) of the MvME-SPFM activation maps were calculated using the trial-level GLM-based activation maps () as the ground truth. These analyses were computed with the independently modulated (IM) option of the 3dDeconvolve program in AFNI that implements an orthogonal least squares estimation for each trial, thus also assuming uncorrelated noise as in our model. Single trial GLM maps (GLM-IM) were obtained from the optimally combined and ME-ICA denoised data, and only negative (i.e., that generate a positive BOLD response) were considered for the computation of the Dice coefficients.
For the MvME-SPFM, the following two strategies for thresholding the AUC timeseries were considered in order to define the corresponding activation maps:
- Static thresholding (ST): The estimates of obtained with the novel MvME-SPFM technique that utilizes stability selection, where the AUC threshold was chosen as the 95th percentile of the histogram of AUC in deep white matter voxels (i.e., a fixed, static threshold), which were labeled after tissue segmentation of the T1-weighted anatomical MRI using 3dSeg in AFNI, and eroding 4 voxels of the resulting white matter tissue mask at anatomical resolution.
- Time-dependent thresholding (TD): The estimates of obtained with the novel MvME-SPFM technique with stability selection, where the AUC threshold varies temporally according to the 95th percentile of the null histogram of AUC at each time-point. This implementation was based on the hypothesis that a time-dependent threshold would be able to better control for widespread spurious deconvolved changes in , for instance due to head motion or deep breaths.
Note the ST and TD thresholding strategies can be applied in the analysis of single-echo and multi-echo fMRI data.
Comparison with Another State-of-the-Art Multivariate Deconvolution Method¶
In order to evaluate how the MvME-SPFM algorithm compares with another state-of-the-art multivariate deconvolution method, Hemolearn Cherkaoui et al., 2021 was chosen, a recently proposed multivariate semi-blind deconvolution method that can estimate the HRF and the neuronal signal in a paradigm-free setting and that has been shown to faithfully capture intrinsic functional connectivity networks at the subject level. This technique introduces a low-rank constraint to learn both temporal atoms (with ) and their corresponding spatial maps, which encode various functional networks, each of them with their specific neural activation profile. Hence, HemoLearn models the brain activity as a linear combination between the neural activations and the spatial patterns , where is the total number of TRs in the data and is the number of voxels. The BOLD fMRI signal model is then given by the convolution between an estimated regional HRF and the activation as:
Thus, the minimization problem proposed by HemoLearn can be described as:
The practical implementation of Hemolearn --which is available at
https://
Results¶
The output of deconvolution algorithms such as ME-SPFM and the proposed MvME-SPFM is a 4D dataset that matches the dimensions (both spatial and temporal) of the input data, i.e., it is a movie of the estimated maps. In addition, the use of stability selection generates the area under the curve (AUC) 4D output dataset, which indicates the probability of having a neuronal-related event at each time-point for every voxel in the brain.
Figure 2 depicts the area under the curve (AUC) time-series and maps obtained with stability selection for in representative voxels of each task in the paradigm (indicated with a cross in the maps), where the AUC maps correspond to single time-points signaled by the blue arrows. The AUC time-series of the ST and TD thresholding approaches are shown on top of the original AUC time-series. The AUC maps depict spatial patterns of where regions that are typically involved in the tasks show higher probabilities of having neuronal-related activity compared with other brain regions.
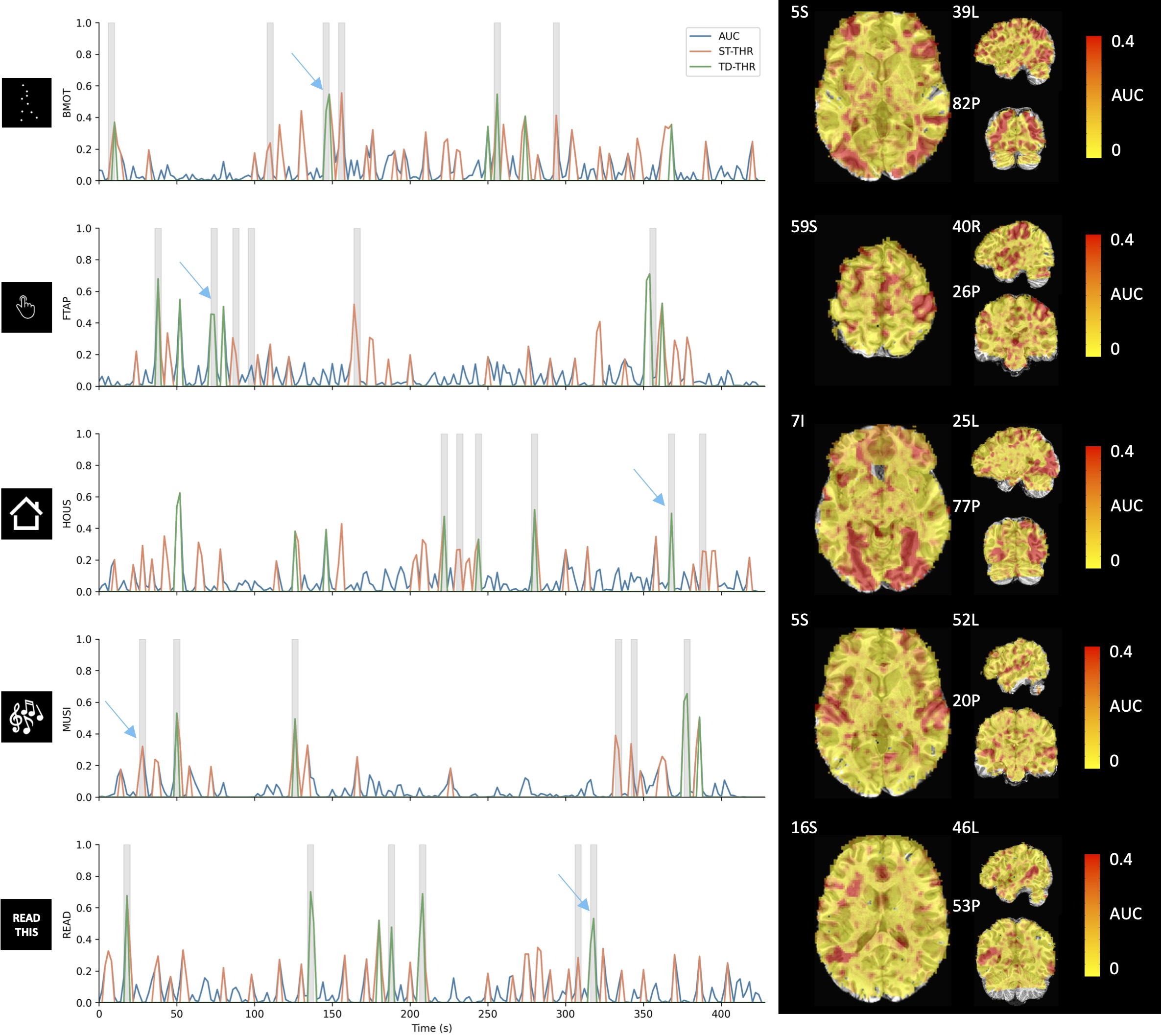
Figure 2:Left: Original (blue), ST thresholded (orange) and TD thresholded (green) AUC time-series for a representative voxel for each task in the paradigm (). Note that the three time-series are overlaid; i.e., the static and time-dependent time-courses are thresholded versions of the original AUC. Gray blocks depict the onset and duration of each trial. Right: AUC maps at the time-points signaled by the blue arrows.
Figure 3 displays the comparison of the maps obtained by solving the inverse problem in Eq. 5 with a fixed selection of λ (1st row) and with the use of stability selection (2nd, 3rd and 4th rows) for . The maps obtained with a fixed selection of λ equal to the noise estimate of the first echo volume (1st row) are very sensitive to the selection of ρ. Similar observations were obtained with other values of λ. With a selection of , only the -norm regularization term is applied, which produces maps with few non-zero coefficients. With , only the -norm spatial regularization is applied, which yields a map that covers the entire brain and does not exhibit a spatial pattern in concordance with the task. However, a selection of yields a map that is more similar to the activity maps often observed when participants are asked to look at the image of a house, depicting negative in bilateral fusiform regions. In contrast, the use of stability selection yields AUC maps (row 2) and the corresponding maps after each thresholding strategy (rows 3-4) reveal activation patterns concordant with those often seen for viewing houses regardless of the selection of ρ. In other words, the maps obtained with stability selection are less sensitive to the selection of ρ while obviating the need to choose λ. In fact, the spatial correlations between the AUC maps for each pair of ρ’s were nearly equal to 1 for all time points (average correlations are 0.97 between , 0.98 between , and 0.97 between ). In addition, it can be seen that using a TD threshold yields BOLD signal changes that are more confined to the expected areas in bilateral fusiform cortices than the ST threshold. Due to the high similarity of the AUC maps for any value of ρ, only the results for are discussed hereinafter.
Figure 3:Comparison of the maps obtained with a fixed selection of λ (row 1) and the use of stability selection (rows 2-4: AUC, stability selection with static thresholding (ST), and stability selection with time-dependent thresholding (TD)) for (column 1), (column 2), and (column 3). These maps correspond to a single-trial event of the house-viewing task (HOUS).
Figure 4 provides an in-depth view of how the time-dependent thresholding operates when motion- and respiration-related artifacts are present in the data. The grayplot Power, 2017 in Figure 4A clearly shows bands spanning throughout the entire brain that illustrate significant changes in the amplitude of the signal. The source of these signal changes can be attributed to head motion events (see Euclidean norm in Figure 4C) and deep breaths (see arrows for respiration volume signal Chang et al., 2009 in Figure 4D). The respiration-related events cause a drop in the global signal (see Figure 4B) seconds after the peak in the respiration volume signal. Interestingly, our results show a decrease in the equivalent ST percentile that corresponds to the 95th TD threshold (Figure 4E) at the instances of these large respiratory-related events. This decrease can also be observed in the corresponding AUC value of the TD thresholding strategy as shown in Figure 4F. The distributions of AUC values at the time-points with respiratory- and motion-related artifacts have a shorter tail than the distribution of the AUC values at the time-points where subjects performed the task. Hence, in these events the TD thresholding strategy is able to adjust the threshold so that the final estimates of specifically capture task-activated voxels while excluding voxels that are affected by artifacts. The higher specificity of the TD thresholding strategy can be clearly seen in the ROC values shown in Figure 4H-L. The use of stability selection with the TD threshold yields more specific estimates of than with ST thresholding or the original ME-SPFM method, while the sensitivity is slightly reduced. On the other hand, the use of stability selection with a ST threshold improves the sensitivity of the estimates compared to the original ME-SPFM technique while preserving its specificity.
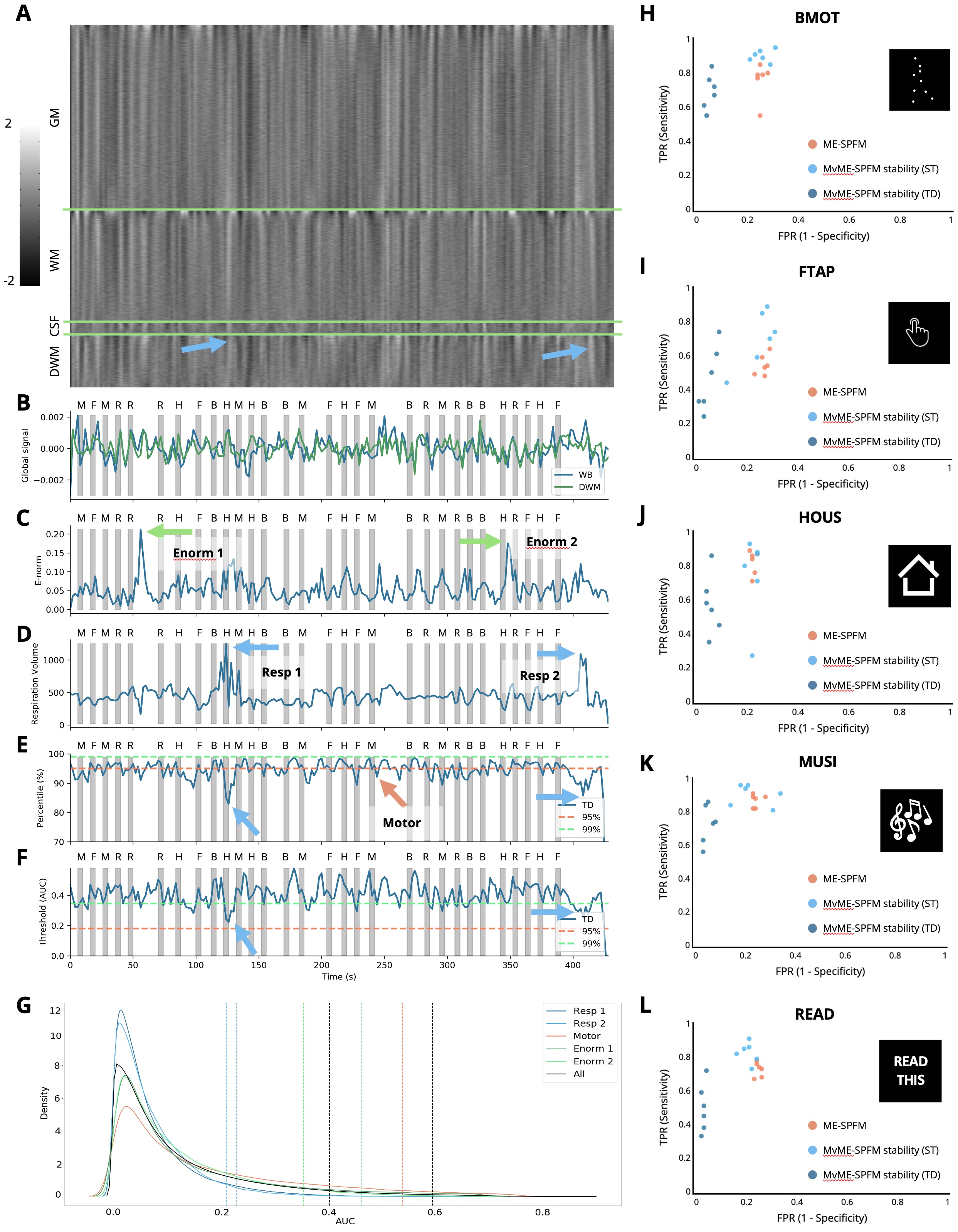
Figure 4:Representative subject with motion and respiration artifacts. A: Grayplot of the second echo volume. The grayplot is divided into 4 sections: gray matter (GM), white matter (WM), cerebrospinal fluid (CSF), and deep white matter (DWM). B: Time-series of the global signal calculated in the whole brain (WB, blue) and the deep white matter (DWM, green). C: Euclidean norm (e-norm) of the temporal derivative of the realignment parameters. D: respiration volume signal. E: AUC percentile corresponding to the time-dependent threshold (lines at 95th and 99th percentiles are shown for reference). F: AUC values corresponding to the time-dependent threshold are shown in blue. The horizontal dashed lines indicate the 95th (orange) and 99th (green) percentiles corresponding to ST thresholding. Gray bars in B-F indicate the onset and duration of each trial in the paradigm, with their respective initials on top. Blue arrows point out two respiration-related events, green arrows point out two motion-related events, and the orange arrow points out a finger-tapping event. G: Probability density functions (estimated by kernel density estimate) of the AUC values corresponding to the instances of the two respiratory-related events (blue lines), a representative time-point of one finger-tapping trial (orange line), the two largest peaks in the e-norm trace (green lines), and the overall AUC distribution (black). The corresponding coloured vertical dashed lines indicate the AUC value for the 95th percentile of the TD thresholding approach, along with the 95th and 99th AUC values of ST thresholding. H-L: Receiver operating characteristic (ROC) values for the original ME-SPFM (orange), and proposed MvME-SPFM technique with the use of stability selection with the ST (light blue) and TD (dark blue) thresholding approaches for this dataset. The ROC plots depict the sensitivity and specificity of the methods at correctly estimating the activity maps that correspond to the 6 trials of each task in the paradigm.
Figure 5 depicts the time-series of the estimated and denoised BOLD, i.e., convolved with the HRF, for a representative voxel of each task for the subject depicted in Figure 4 and Figure 7 and compared to a reference voxel in the lateral ventricles. The location of the voxels is shown in the corresponding maps in Figure 7. The ST thresholding approach detects events of the activity-inducing signal that correctly match the timings of the stimuli (i.e., high temporal sensitivity), but also shows events that occur in the resting state and do not coincide with any activity-evoking trial. Based on comparison with the events detected in the time series extracted from the lateral ventricles, it can be conjectured that some of these events might be due to artifactual and physiological fluctuations that remain in the signal after preprocessing. On the other hand, values estimated with the TD thresholding approach match the timings of the stimuli almost perfectly with few missed trials (high temporal specificity). This is supported by the few events obtained for the reference voxel in the ventricles. Likewise, the denoised BOLD time-series obtained with the TD thresholding approach clearly describes signal changes associated with the trials, whereas the denoised BOLD time-series estimated with the ST thresholding strategy fits the original data very closely, which could be interpreted as a signature of overfitting.
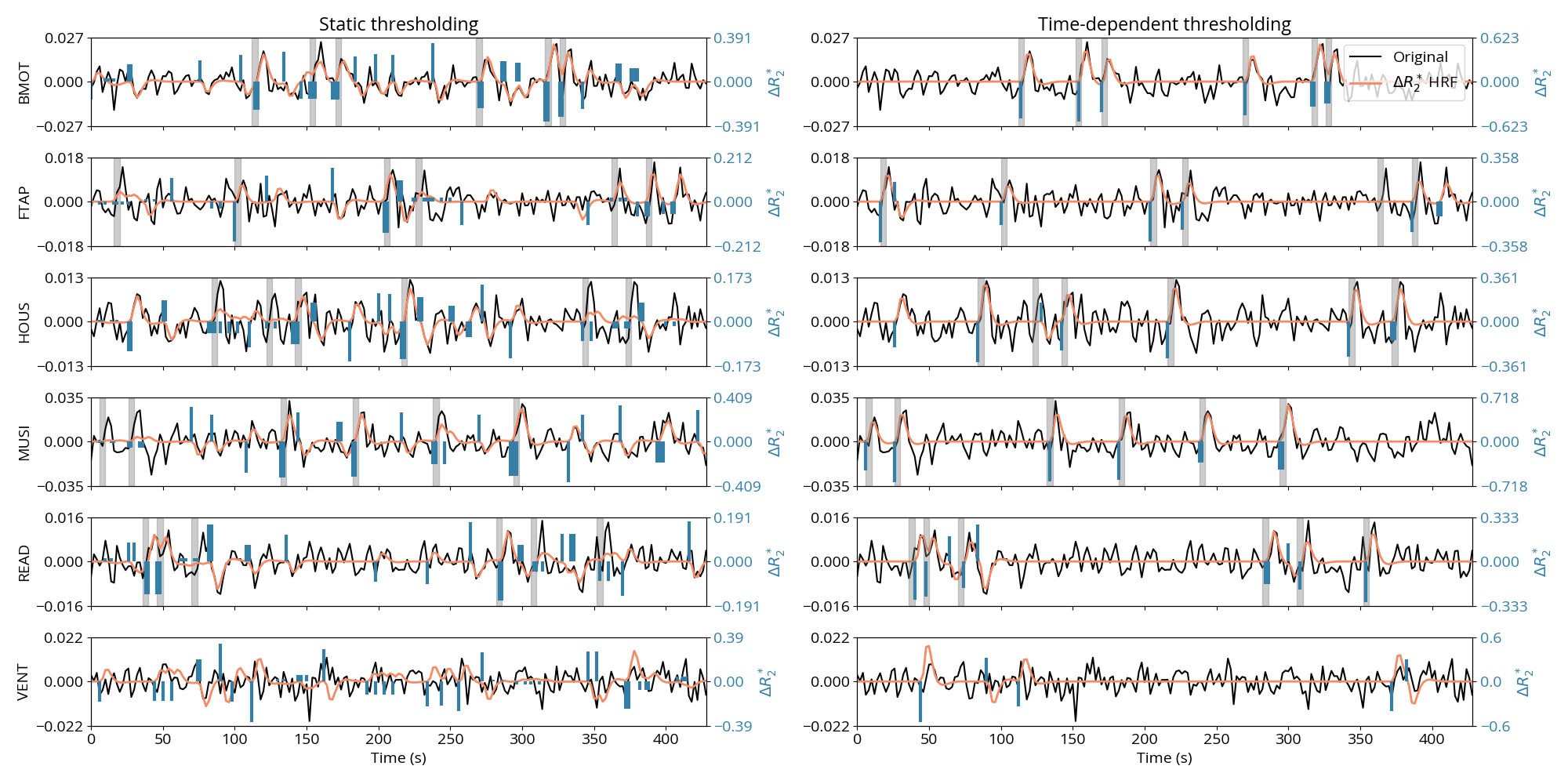
Figure 5:Comparison of the estimated (blue) and denoised BOLD (orange), i.e., convolved with the HRF, time-series when employing the ST (left) and TD (right) thresholding approches, for representative voxels of each task (rows) as well as one voxel from the lateral ventricle for reference. The estimates shown here were obtained with . The preprocessed time series is shown in black. The gray bars indicate the onset and duration of each trial for each task of the experimental paradigm.
Figure 7 illustrates the activation maps of representative single-trial events of each task for the same subject depicted in Figure 4. The activation maps of the proposed MvME-SPFM formulation were compared using the two thresholding approaches with the activation maps obtained with a single-trial GLM and the previous ME-SPFM approach. While all PFM methods exhibit activation maps that highly resemble those obtained with the single-trial GLM analysis, differences between the methods can be observed. For instance, although the use of stability selection with a ST thresholding approach yields maps with clusters of activation of comparable size and location to those found with ME-SPFM, in certain noisy trials (e.g., see HOUS-Trial 1), the ST-thresholding MvME-SPFM maps can yield reduced spatial specificity, probably related to spurious, scattered changes in . Across all tasks, the maps obtained with TD thresholding exhibit a notably larger resemblance to the single-trial GLM, showing higher spatial specificity and lower sensitivity compared to the other two PFM methods.
To further evaluate the proposed MvME-SPFM, the motor task of a single subject (100206) extracted from the Human Connectome Project (HCP) dataset Van Essen et al., 2013 was analyzed. The data was 3 min 24 s long (after removing the first 10 seconds for steady magnetization) with a TR of 0.72 s, a multi-band factor of 8 and a spatial resolution of mm3. The images were already preprocessed using a standard HCP pipeline including realignment, coregistration, spatial normalization and smoothing. The task was composed of 5 blocks of 12 s each, preceded by a 3 s cue indicating the task to be performed by the participant. The conditions in each 5-second block were: left hand finger tapping, right hand finger tapping, left foot movement, right foot movement, and tongue movement. The process was repeated once more, resulting in a total of 10 blocks. We adjusted the signal model in Eq. 3 to be used with single-echo data as described in Gaudes et al., 2013Uruñuela et al., 2023.
The accurate performance of the proposed MvME-SPFM method observed in the multi-echo fMRI data is consistent with the results found in the single-echo data from the Human Connectome Project. Figure 6 depicts the single-trial activity maps obtained with a GLM and the proposed approach with stability selection and both ST and TD thresholding. In general, the activity maps obtained with the proposed method are highly comparable to the single-trial GLM activation maps. Importantly, the proposed method showed a larger sensitivity to detect the activity evoked by the motor task for certain trials than the timing-aware GLM analysis. For instance, the Mv-SPFM activation maps of the second trial for the left hand finger tapping condition shows more BOLD activity in motor regions of the right precental gyrus, which is barely seen in the corresponding single-trial GLM map.
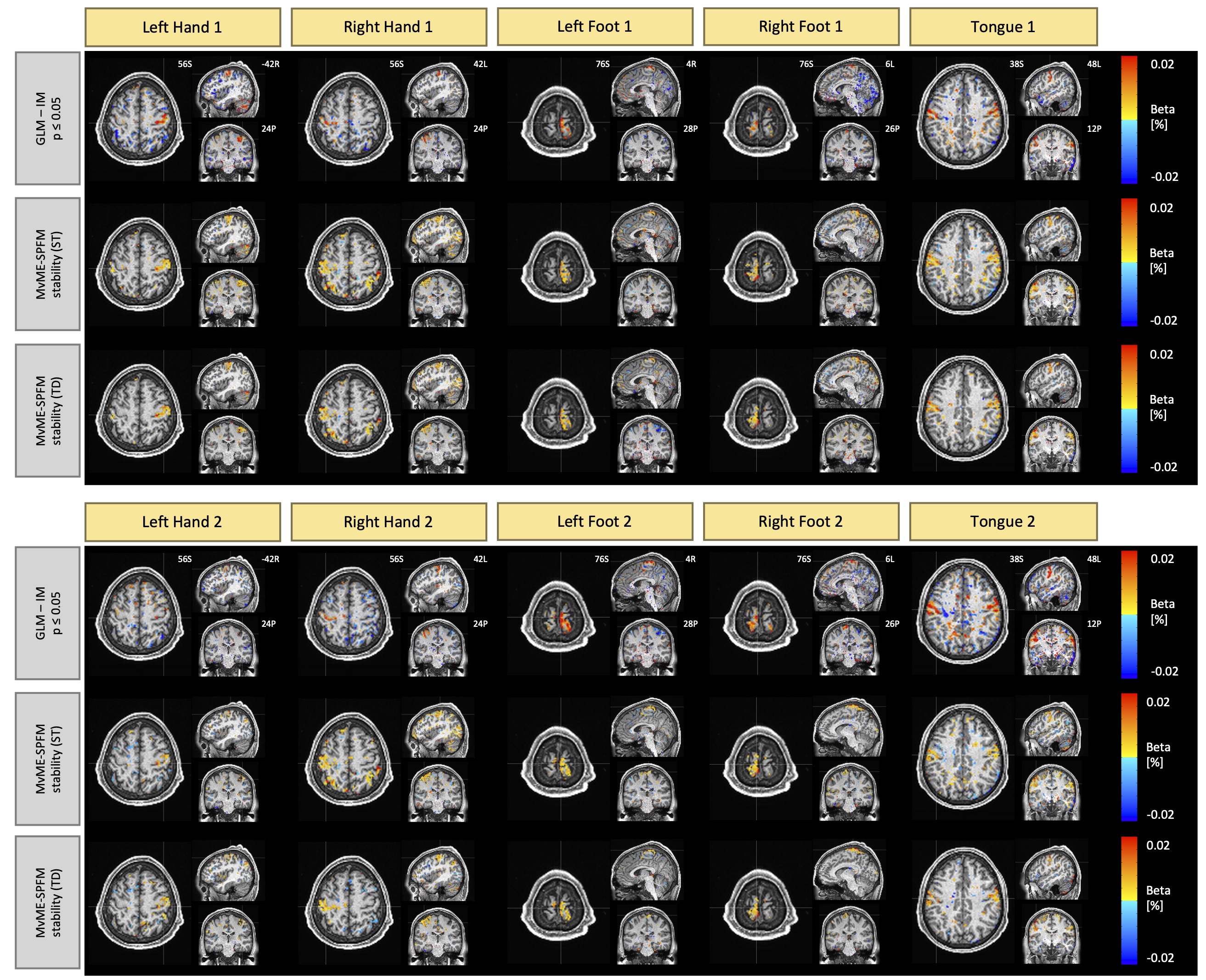
Figure 6:Single-trial activity maps estimated for the single-echo motor task data from the Human Connectome Project.Row 1 depicts the activation maps obtained with a single-trial GLM (), row 2 depicts the maps detected with the novel Mv-SPFM technique with stability selection, and a static threshold (ST), and row 3 illustrates the results using a time-dependent threshold (TD). The activity maps corresponding to the first trial are shown on top, and the activity maps corresponding to the second trial are shown on the bottom.
Figure 7:Comparison of single-trial activation maps obtained with a GLM (row 1) thresholded at , the original ME-SPFM formulation with a fixed selection of λ (row 2), the novel MvME-SPFM technique with stability selection, and a static threshold (ST, row 3), and using a time-dependent threshold (TD, row 4). A representative trial is shown for each task. All the maps correspond to the same subject and run shown in Figure 4.
As illustrated in Figure 8, the Dice coefficient between the estimated single-trial activity maps and the reference GLM activity maps () demonstrates only a slight improvement over the original ME-SPFM formulation when employing an ST thresholding approach with the novel MvME-SPFM technique. In contrast, the Dice coefficients obtained with TD thresholding show a very notable increase of nearly 50% in the median of the distribution of Dice coefficients compared with the original ME-SPFM approach. Similarly, the sensitivity and specificity distributions of ST thresholding demonstrate a slight improvement with respect to the original ME-SPFM formulation. On the other hand, the use of TD thresholding offers nearly perfect specificity () at the cost of reduced sensitivity across all experimental conditions. Hence, increasing the specificity of the maps is more beneficial for increasing the concordance with the GLM maps than increasing the sensitivity.
The receiver operating characteristic (ROC) values in Figure 9 corroborate the previous
observations regardless of the value of ρ used in the MvME-SPFM method. The estimates obtained
with the ST threshold reveal an overall higher sensitivity and a slightly higher specificity
compared to the original ME-SPFM technique. In contrast, the ROC values for the TD thresholding
approach show a clear improvement in specificity but lower sensitivity. These findings are in line
with the results shown in Figure 3, Figure 7 and
Figure 5, as the Dice and ROC values certify that the use of stability selection
yields robust activation maps regardless of the selection of the spatial regularization term ρ
and obviating the need to choose the temporal regularization parameter λ. An interactive
version of Figure 8 and Figure 9 is available in the following GitHub repository:
https://
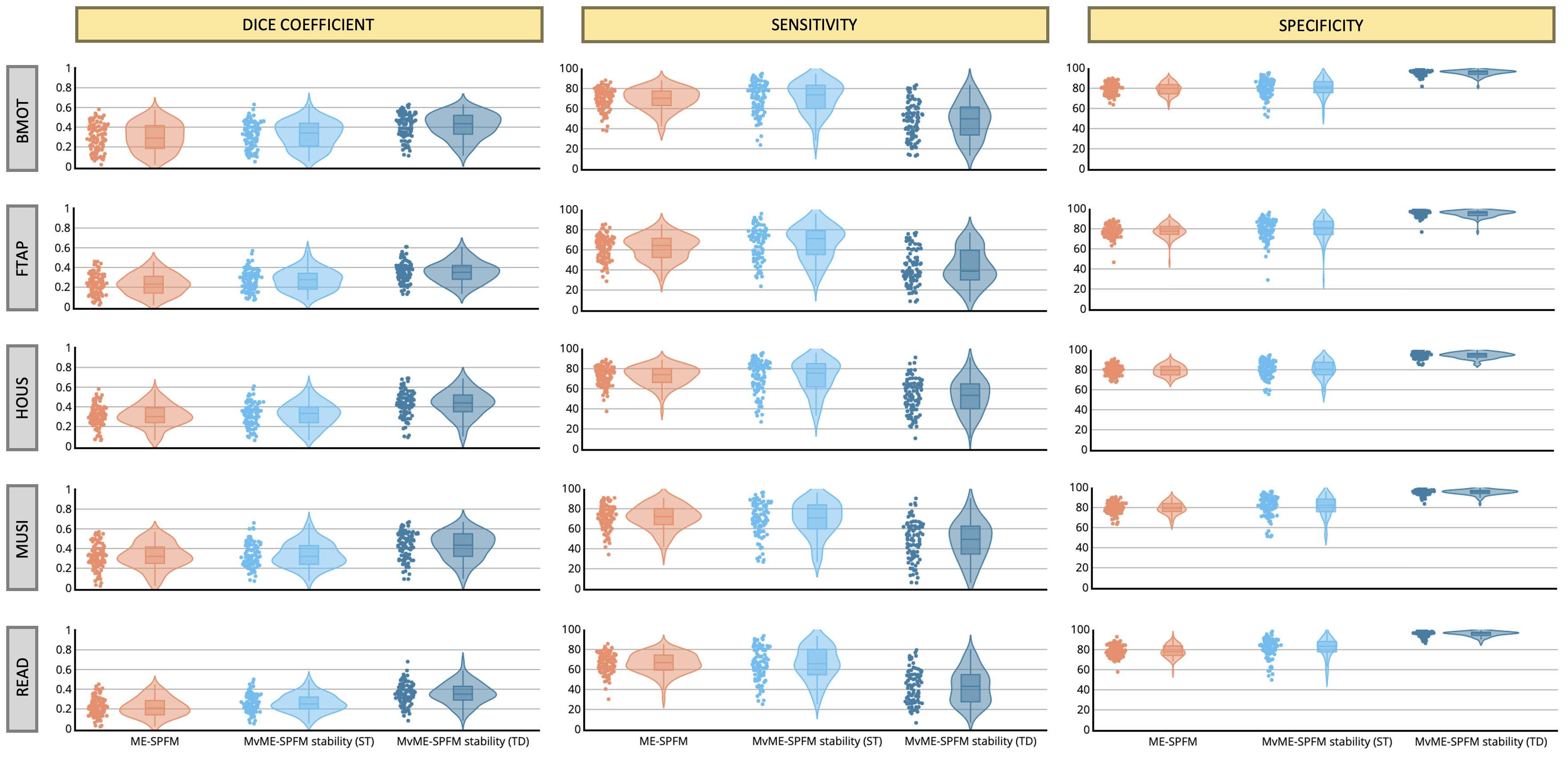
Figure 8:Dice coefficient (i.e., spatial overlap), sensitivity and specificity coefficients of the single-trial activation maps for each of the experimental conditions obtained with ME-SPFM, MvME-SPFM with stability selection and a static thresholding approach (ST), and MvME-SPFM with stability selection and a time-dependent thresholding approach (TD). These metrics were obtained with a selection of . Reference activation maps were obtained with a single trial GLM analysis and thresholded at uncorrected . The density plot shows the shape of the distribution of the Dice coefficients, and the box plot depicts the median with a solid line, with each box spanning from quartile 1 to quartile 3. The whiskers extend to 1.5 times the interquartile range.
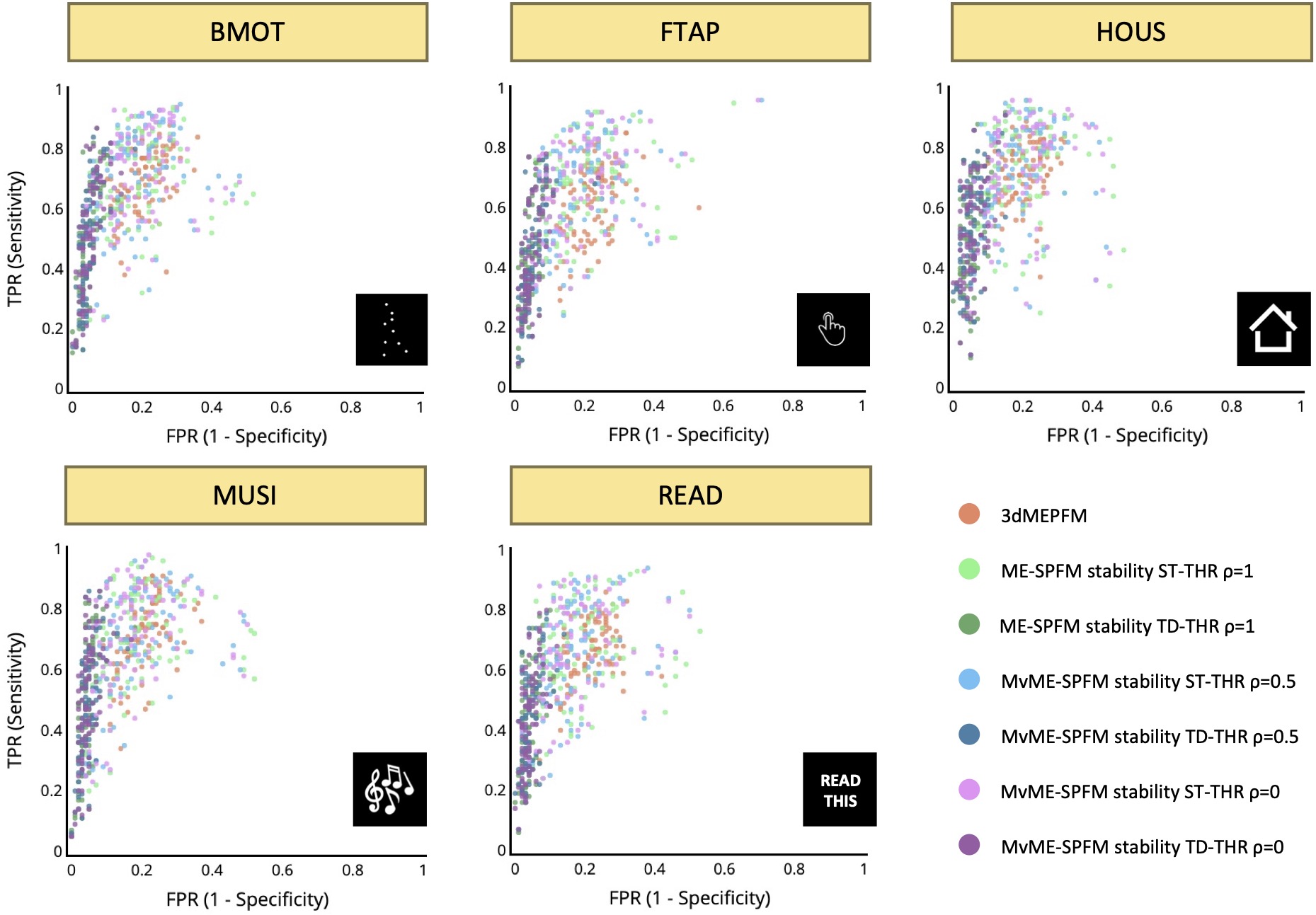
Figure 9:Receiver operating characteristic (ROC) values with the sensitivity and specificity of each single trial’s activation map for all conditions and the reference map obtained with a single-trial GLM. Different colors are used for the different analyses: the original ME-SPFM, and the novel MvME-SPFM approach using stability selection with the spatial regularization parameter set to and the two different thresholding methods: static (ST) and time-dependent (TD). In each analysis each dot represents a single trial, depicting all trials across all datasets, and the centroids across all the single trials are also shown for the three analyses.
These findings are further corroborated by the average activity maps across trials, sessions and subjects for each condition in the task shown in Figure 10. The maps obtained with the novel MvME-SPFM technique with stability selection and TD thresholding show a high resemblance to the average of the single-trial GLM activation maps (3dDeconvolve with independently-modulation (IM) option in AFNI, thresholded at ). Interestingly, the MvME-SPFM approach seems to offer improved detection of neuronal-related activity than the GLM approach for certain conditions, for example, in the voxels of the left inferior frontal gyrus (i.e., Broca’s region) and left posterior superior temporal gyrus (i.e., Wernicke’s region) for the reading condition, where the GLM maps show a smaller cluster of activation.
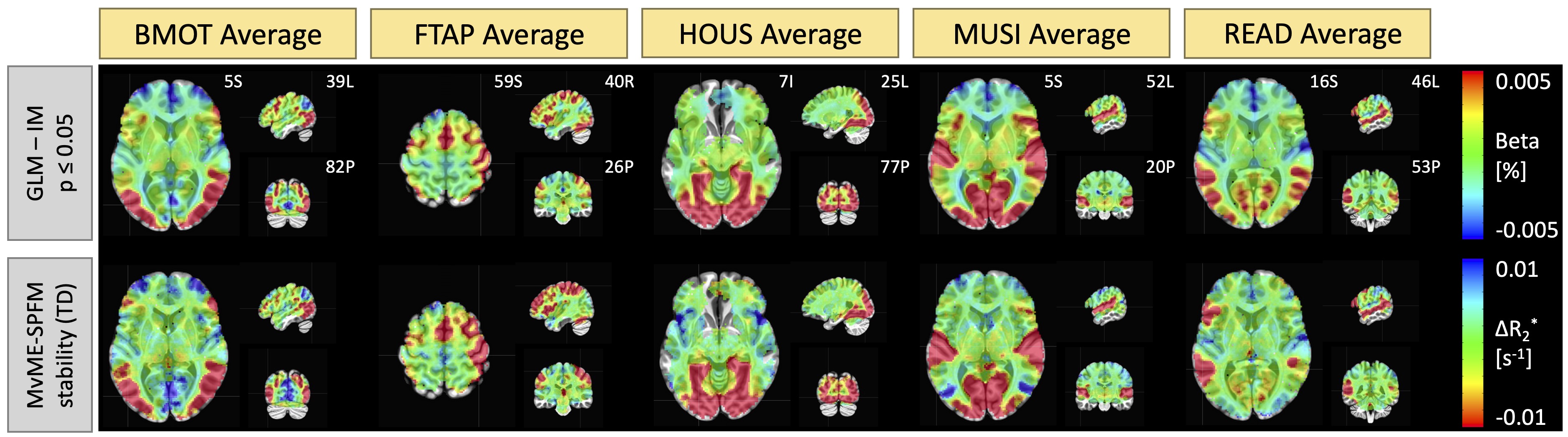
Figure 10:Average activity maps across trials, sessions and subjects for each condition in the task obtained with (top) a single-trial GLM analysis (independently modulated, IM) and the proposed MvME-SPFM algorithm with stability selection, and a time-dependent threshold (TD).
Figure 11 shows the comparison with the HemoLearn algorithm Cherkaoui et al., 2021. Panels A and B illustrate the difficulty of selecting a suitable number of components for Hemolearn since the number of components giving the highest correlation to the session-level GLM was different for each condition. The timecourses of the estimated activity-inducing signal in C show that Hemolearn struggles to capture the timings of the task in all conditions, while the MvME-SPFM technique with stability selection and TD thresholding is able to capture the expected activity-inducing signal with barely missing any of the events in the task. These observations are also visible in the activity maps shown in D, where the activity maps obtained with the MvME-SPFM technique with stability selection and TD thresholding are comparable to those obtained with the GLM (see Figure 7), while the maps of the Hemolearn components that had the highest correlation with the session-level GLM maps do not show a clear activity pattern related to the task.
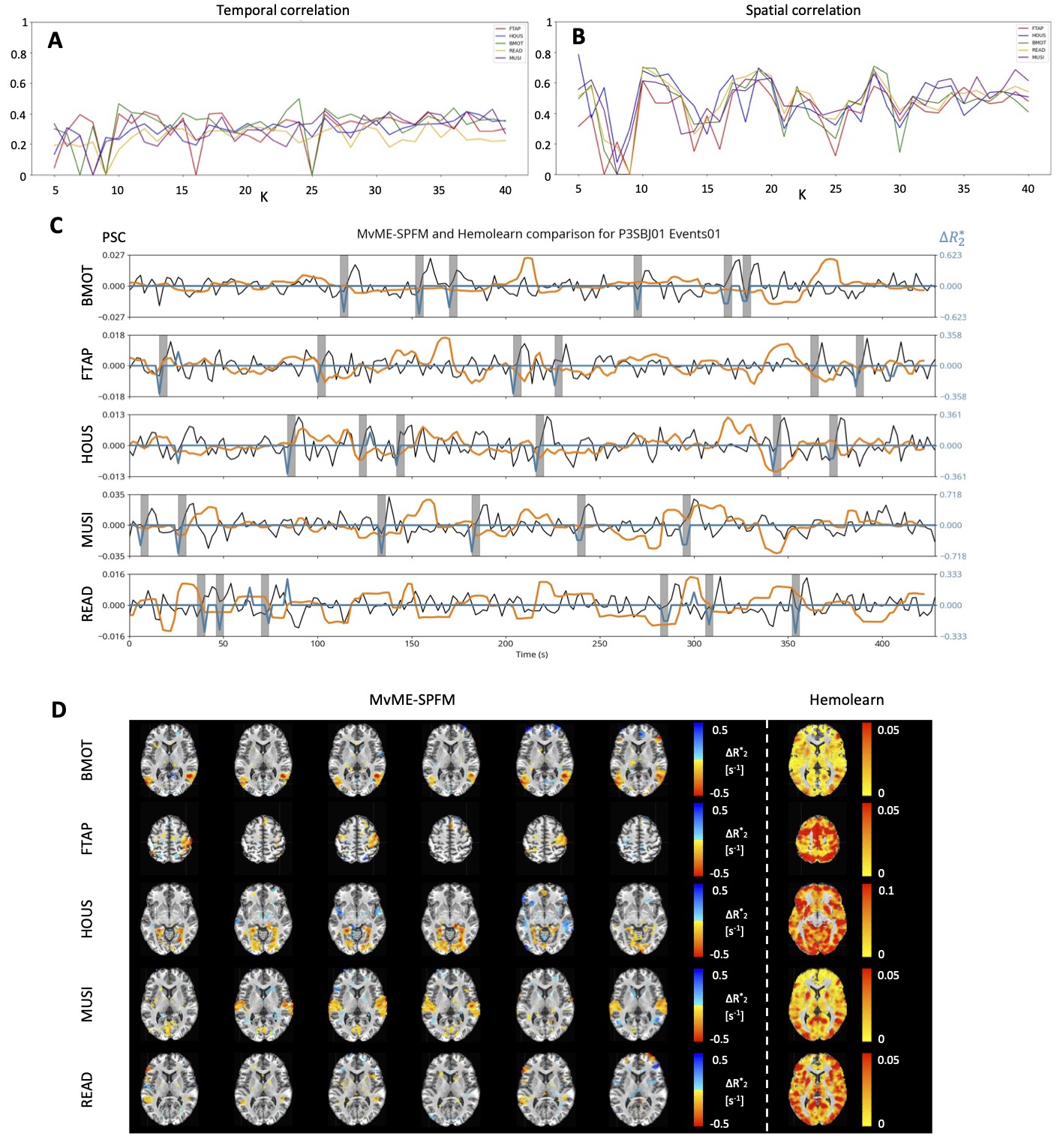
Figure 11:Comparison of the activity maps obtained with the novel MvME-SPFM technique with stability selection, and a time-dependent threshold (TD) with Hemolearn. Session 1 of subject P3SBJ01 was used for this comparison. A and B show the highest correlation to the session-level GLM regressor and activity map respectively obtained by Hemolearn for each condition in the task (FTAP in red, HOUS in dark blue, BMOT in green, READ in yellow, and MUSI in purple) and the range of K components explored (). C illustrates the timecourses of MvME-SPFM (blue, ) and Hemolearn-estimated (orange, percent signal change) activity-inducing signal in a representative voxel for each condition. The gray bars show the onset and duration of each trial within a condition, and the measured fMRI signal is shown in percent signal change (PSC) in black. D compares the trial-level activity maps estimated with MvME-SPFM with the Hemolearn activity map with the highest correlation with the session-level GLM map across the explored range of K components. Every row in C and D correspond to the different conditions in the task.
Discussion and Conclusion¶
The proposed whole-brain (i.e., multivariate) formulation for hemodynamic deconvolution of multi-echo fMRI data with the use of stability selection achieved a closer agreement with the activation maps obtained with a single-trial GLM analysis than the original ME-SPFM method Caballero-Gaudes et al., 2019 and other state-of-the-art multivariate deconvolution method like Hemolearn Cherkaoui et al., 2021, while obviating the need to select the temporal regularization parameter λ (as shown in Figure 7 and Figure 11).
Furthermore, this chapter demonstrated that the performance of the proposed method was robust not only for the analysis of multi-echo data, but also when analyzing single-echo data, as demonstrated in Figure 6. In addition, our results illustrated that the stability selection procedure also offers robustness against the choice of the spatial regularization parameter ρ, as the AUC maps for different selections of ρ were practically identical, as shown in Figure 3. Hence, although stability selection could be employed with a double selection of the regularization parameters λ and ρ, this can be avoided for computational reasons with little influence in the results. In any case, extending the proposed stability selection technique to other formulations of the hemodynamic deconvolution problem, such as the voxel-wise (i.e., univariate) single-echo Gaudes et al., 2013Uruñuela et al., 2020 described in Chapter 2: Synthesis-Based and Analysis-Based Hemodynamic Deconvolution for fMRI and Chapter 3: Stability-Based Sparse Paradigm Free Mapping, univariate multi-echo Caballero-Gaudes et al., 2019, or low-rank and sparse formulations Uruñuela et al., 2021Cherkaoui et al., 2021 described in Chapter 6: Sparse and Low-Rank Paradigm Free Mapping, is relatively straightforward.
One of the most interesting features of the proposed stability selection procedure is the estimation of the area under the curve (AUC) measure, which provides a new perspective for exploring fMRI data: a 4D movie with the probability of each voxel and time point containing a neuronal-related event. Therefore, the AUC time-series and maps provide complementary information to the estimates of , and serve as a reliability measure. Even though the AUC measures were employed here to produce the final estimates of the activity-inducing signal, they could also be exploited on their own. For instance, they could be exploited to constrain functional connectivity analysis Tagliazucchi et al., 2016Faskowitz et al., 2020 to voxels and instants with a high probability of containing a neuronal-related event. Furthermore, the stability selection and the AUC metric can also be interpreted from a machine learning perspective, where the outputs from a collection of lasso learners are combined with an ensemble regression approach. Alternatively, the stability selection procedure could also be linked to Bayesian approaches where the prior is given by the range of values of the regularization term λ and the total posterior probability of the neuronal event is calculated as the integration of the stability paths, i.e., the AUC (see discussion in Meinshausen & Bühlmann (2010)).
Although the estimation of the AUC eliminates the need to select the spatial and temporal regularization parameters λ and ρ, it requires the use of a thresholding approach given the nature of the AUC measure, which cannot be equal to zero by definition. This chapter adopted two data-driven thresholding strategies, static (ST) and time-dependent (TD), based on the AUC values of a region where no BOLD signal changes related to neuronal activity are assumed to occur (e.g., deep white matter voxels). The use of a static AUC thresholding approach yielded higher sensitivity than the original ME-SPFM method Caballero-Gaudes et al., 2019 while maintaining the specificity as demonstrated in Figure 9. Notably, this improvement was seen in all trials with the exception of one outlier run, regardless of the choice of the spatial regularization parameter ρ. Nevertheless, the use of a time-dependent thresholding approach may be even justified by the increased specificity and nearly perfect retrieval of the activity-inducing signal (row 3 in Figure 5) when motion- and respiration-related artifacts are visible in the data (see arrows in Figure 4). However, the application of the time-dependent threshold may reduce sensitivity at the single-trial level in some cases. Hence, the results shown in Figure 9 encourage the use of the static thresholding approach as an exploratory step before employing the time-dependent threshold. Other thresholding criteria could involve the comparison of AUC values obtained from surrogate (null) data Liégeois et al., 2021 with the AUC values obtained with the original data.
Furthermore, the extension of the original ME-SPFM algorithm from a voxel-wise to a whole-brain (i.e., multivariate) regularized problem paves the way for more refined formulations that exploit the spatial characteristics and information available in fMRI and complementary imaging data into the spatial regularization term in order to improve the estimation of . For instance, the spatial regularization could be constrained within brain regions delineated by commonly used parcellations (e.g., the Schaefer-Yeo atlas) Karahanoğlu et al., 2013 or within neighbouring gray matter voxels Farouj et al., 2017. Other mixed-norm regularization terms could also be investigated in future work to account for alternative models of spatially varying noise SNR, e.g., the octagonal shrinkage and clustering algorithm for regression (OSCAR) Gueddari et al., 2021, which employs a plus a pairwise -norm between voxels instead of a global -norm to account for spatially varying SNR across voxels. Moreover, the multivariate formulation could exploit complimentary multimodal information such as structural connectivity from diffusion-based MRI data Bolton et al., 2019. In addition, the proposed formulation can be easily adapted to model the changes in neuronal activity in terms of its innovations, which can be more appropiate to capture sustained BOLD events as described in Chapter 2: Synthesis-Based and Analysis-Based Hemodynamic Deconvolution for fMRI (see also Uruñuela et al. (2023)).
One limitation of the proposed MvME-SPFM technique is the assumption of a particular shape of the hemodynamic response to construct the HRF matrix for deconvolution in Eq. 3. The proposed model does not account for the variability in the temporal characteristics of the HRF across the brain, which originates from differences in stimulus intensity and patterns, short inter-event intervals, or differences in the HRF shape between resting-state and task-based paradigms Yeşilyurt et al., 2008Sadaghiani et al., 2009Chen et al., 2021Polimeni & Lewis, 2021. To resolve this issue, given that the performance of MvME-SPFM is not time-locked to the trials, the current formulation could be extended to account for variability in the onset of the activity-inducing signal, as well as to introduce flexibility in the model, by employing multiple basis functions Gaudes et al., 2012. Furthermore, our method could be easily employed independently within parcels of any commonly-used atlases with a pre-estimated, localized HRF. Finally, the computational demands involved in the stability selection procedure, which solves the regularization problem in Eq. 5 for a range of λ values on a number of subsampled surrogate datasets, are higher than solving the regularization path and finding an adequate solution via model selection criteria as in ME-SPFM Caballero-Gaudes et al., 2019. At the moment of writing, the method took approximately 10 hours to run on a high-performance computing cluster parallelizing the stability selection procedure so that each surrogate dataset was processed in a different core.
Code and data availability¶
The code and materials used to generate the figures in this work can be found in the following
GitHub repository:
https://
The Python package is available as part of splora in the following GitHub repository:
https://
- Uruñuela, E., Gonzalez-Castillo, J., Zheng, C., Bandettini, P., & Caballero-Gaudes, C. (2024). Whole-brain multivariate hemodynamic deconvolution for functional MRI with stability selection. Medical Image Analysis, 91, 103010. https://doi.org/10.1016/j.media.2023.103010
- Bright, M. G., & Murphy, K. (2013). Removing motion and physiological artifacts from intrinsic BOLD fluctuations using short echo data. NeuroImage, 64, 526–537. 10.1016/j.neuroimage.2012.09.043
- Kundu, P., Voon, V., Balchandani, P., Lombardo, M. V., Poser, B. A., & Bandettini, P. A. (2017). Multi-echo fMRI: A review of applications in fMRI denoising and analysis of BOLD signals. NeuroImage, 154, 59–80. 10.1016/j.neuroimage.2017.03.033
- Bolton, T. A. W., Farouj, Y., Inan, M., & Ville, D. V. D. (2019, April). Structurally-Informed Deconvolution of Functional Magnetic Resonance Imaging Data. 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019). 10.1109/isbi.2019.8759218
- Uruñuela, E., Moia, S., & Caballero-Gaudes, C. (2021, April). A Low Rank and Sparse Paradigm Free Mapping Algorithm For Deconvolution of fMRI Data. 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI). 10.1109/isbi48211.2021.9433821