This chapter was published as Uruñuela et al. (2021).
Current deconvolution algorithms for functional magnetic resonance imaging (fMRI) data are hindered by widespread signal changes arising from motion or physiological processes (e.g. deep breaths) that can be interpreted incorrectly as neuronal-related hemodynamic events. This work proposes a novel deconvolution approach that simultaneously estimates global signal fluctuations and neuronal-related activity with no prior information about the timings of the blood oxygenation level-dependent (BOLD) events by means of a sparse and low rank decomposition algorithm. The performance of the proposed method is evaluated on simulated and experimental fMRI data, and compared with state-of-the-art sparsity-based deconvolution approaches and with a conventional analysis that is aware of the temporal model of the neuronal-related activity. This chapter demonstrates that the novel sparse and low-rank paradigm free mapping (SPLORA-PFM) can estimate global signal fluctuations related to motion in the task, while estimating the neuronal-related activity with high fidelity. The open-source Python package for SPLORA is available at https://github.com/ParadigmFreeMapping/splora.
Introduction¶
As noted in previous chapters of this thesis, hemodynamic deconvolution algorithms of functional magnetic resonance imaging (fMRI) data aim to estimate blood oxygenation level-dependent (BOLD) events with no prior knowledge of their timing. These algorithms can be specially useful when the information about the timing of the neuronal activity that drives the BOLD events is unknown, inaccurate or insufficient (e.g., resting-state, naturalistic paradigms, clinical conditions). However, the performance of existing deconvolution approaches can be hampered considerably in presence of global, widespread signal changes due to head jerks, hardware artefacts or prominent non-neuronal physiological events (e.g., deep breaths) Power et al., 2017. Signal artefacts due to head motion and hardware malfunction can be reduced by means of denoising algorithms, such as ICA-AROMA Pruim et al., 2015 or ME-ICA Kundu et al., 2012, or can be compensated with a multi-echo Paradigm Free Mapping formulation Caballero-Gaudes et al., 2019. However, global physiological events are more difficult to compensate during data preprocessing Power et al., 2018 and can be misinterpreted as neuronally related since their temporal signature can closely resemble the hemodynamic response function (HRF) assumed in the deconvolution model to describe neurovascular coupling.
This chapter proposes a new Paradigm Free Mapping algorithm for spatio-temporal deconvolution of fMRI data that is capable of simultaneously estimating global signal fluctuations and neuronal-related activity based on a sparse and low-rank decomposition approach. The proposed algorithm extends the formulation of the multivariate-sparse Paradigm Free Mapping (Mv-SPFM) introduced in Chapter 4: Whole-Brain Multivariate Deconvolution for Multi-Echo Functional MRI by using a regularized estimator consisting of the same structured sparsity promoting norm but adding a low-rank-promoting nuclear-norm Otazo et al., 2015.
Sparse and Low-Rank Paradigm Free Mapping¶
Let us consider that the whole-brain fMRI data where is the number of volumes and is the number of voxels of the acquisition can be decomposed into three terms, i.e.,
where the neuronal-related component is the convolution
of voxel-specific neuronal-related signals with the Toeplitz matrix
with shifted HRFs in its columns (i.e.
similar to the formulation used for multivariate Paradigm Free Mapping
Uruñuela et al. (2024)), the global fluctuations can be captured as the sum of
spatially widespread (i.e.\ global) low-rank components
where and denote their corresponding spatial and temporal
signatures, and represents additional white Gaussian noise.
The following multivariate regularized least-squares problem is proposed to estimate both the neuronal-related signals and the global components:
where denotes the Frobenious norm, the +-norm term enforces temporal sparsity and spatial structure on the estimate of the neuronal-related activity and ρ controls the tradeoff between both terms Gramfort et al., 2011Uruñuela et al., 2024 and is a diagonal matrix with voxel-specific non-negative regularization parameters that balances the sparsity of and data fidelity for each voxel. In addition, the nuclear-norm encourages the estimation of low-rank components where the non-negative regularization parameter controls the number of low-rank components.
Here, ρ is empirically set to 0.8 to enforce structure in the spatial domain and maintain the sparsity of the estimates. For each voxel, is set equal to the median absolute deviation estimate of the noise standard deviation from the fine-scale wavelet coefficients of the voxel time series (Daubechies, order 3). After the singular value decomposition (SVD) of the data, is set to select low-rank components corresponding to the largest eigenvalues showing a difference of at least 10% with respect to the next eigenvalue.
The optimization problem in Eq. 2 is solved via monotone FISTA with variable acceleration (MFISTA-VA, Zibetti et al. (2018)) as shown in Figure 1.

Figure 1:Pseudocode for Monotone FISTA with Variable Acceleration.
Methods¶
Simulated Data¶
1000 voxels were simulated including two groups of 50 voxels with a known BOLD signal, whereas the remaining voxels did not contain any BOLD signal. For each voxel, different signal sources representing motion-related, thermal and physiological noise were added following Gaudes et al., 2013, as well as two global low-rank components (see Figure 2 A) with a random voxelwise amplitude simulating widespread signal changes due to two deep breaths Power et al., 2018 and large amplitude spikes mimicking spin-history artefacts due to head jerks, respectively.
The performance of the proposed SPLORA-PFM algorithm was asssesed on different signal to noise ratio (SNR) settings and with different ratios of voxels with BOLD signals to total number of voxels (denoted as BOLD/total voxels ratio). Four different algorithms based on Eq. 2 were evaluated depending on the regularization parameters:
- SPFM with no low-rank estimation and no spatial regularization (SPFM, , )
- MV-SPFM with no low-rank estimation (MV-SPFM, , )
- SPLORA-PFM algorithm with only the L1-norm (LR+SPFM, )
- SPLORA-PFM algorithm ()
These were benchmarked against the original univariate SPFM algorithm with regularization parameter selected according to the Bayesian Information Criterion (SPFM-BIC, Gaudes et al. (2013)). Note that both the SPFM algorithm with and and the original SPFM-BIC algorithm operate voxelwise, except the regularization parameters are chosen differently.
True and false positive and negative values were calculated for the ROC values comparing the estimated activity-inducing signal with the simulated (binary) activity-inducing signal (ground truth) as follows: a TR was deemed as a true positive (TP) when the estimated and simulated values were both non-zero; a TR was treated as true negative (TN) when both the estimated and simulated values were zero; false positives (FP) were given to those TRs with a non-zero estimated value when the simulated value was zero; and false negatives (FN) were considered when the estimated value was zero but the simulated value was non-zero. Sensitivity and specificity values were calculated as and respectively.
Experimental Data¶
Nine healthy subjects were scanned in a 3T Siemens Prisma MR scanner in ten sessions at the same hour and day of the week. T2*-weighted multi-echo fMRI data was collected with a multiband (MB) multiecho gradient echo planar imaging sequence (340 scans, 52 slices, Partial-Fourier=6/8, voxel size=2.4x2.4x3 mm\textsuperscript{3}, TR=1.5 s, TEs=10.6/28.69/46.78/64.87/82.96 ms, flip angle=70o, MB factor=4, GRAPPA=2). During the fMRI acquisition, subjects performed a motor task consisting of five different movements (left-hand finger tapping, right-hand finger tapping, moving the left toes, moving the right toes and moving the tongue). These conditions were randomly intermixed every 16 seconds, and were only repeated once the entire set of conditions were presented. For this work, only the first two sessions were selected to evaluate the algorithm.
Data preprocessing was carried out with AFNI Cox, 1996 including volume realignment, optimally combining the echo time datasets with \textit{tedana} DuPre et al., 2021, detrending of up to 5th-order Legendre polynomials, spatial smoothing with a Gaussian kernel of 3 mm Full Width Half Maximum, and normalization to signal percentage change. Based on the simulation results, preprocessed data was analyzed with the novel SPLORA-PFM algorithm with , and and were selected as described in Sparse and Low-Rank Paradigm Free Mapping.
Results and Discussion¶
Simulated Data¶
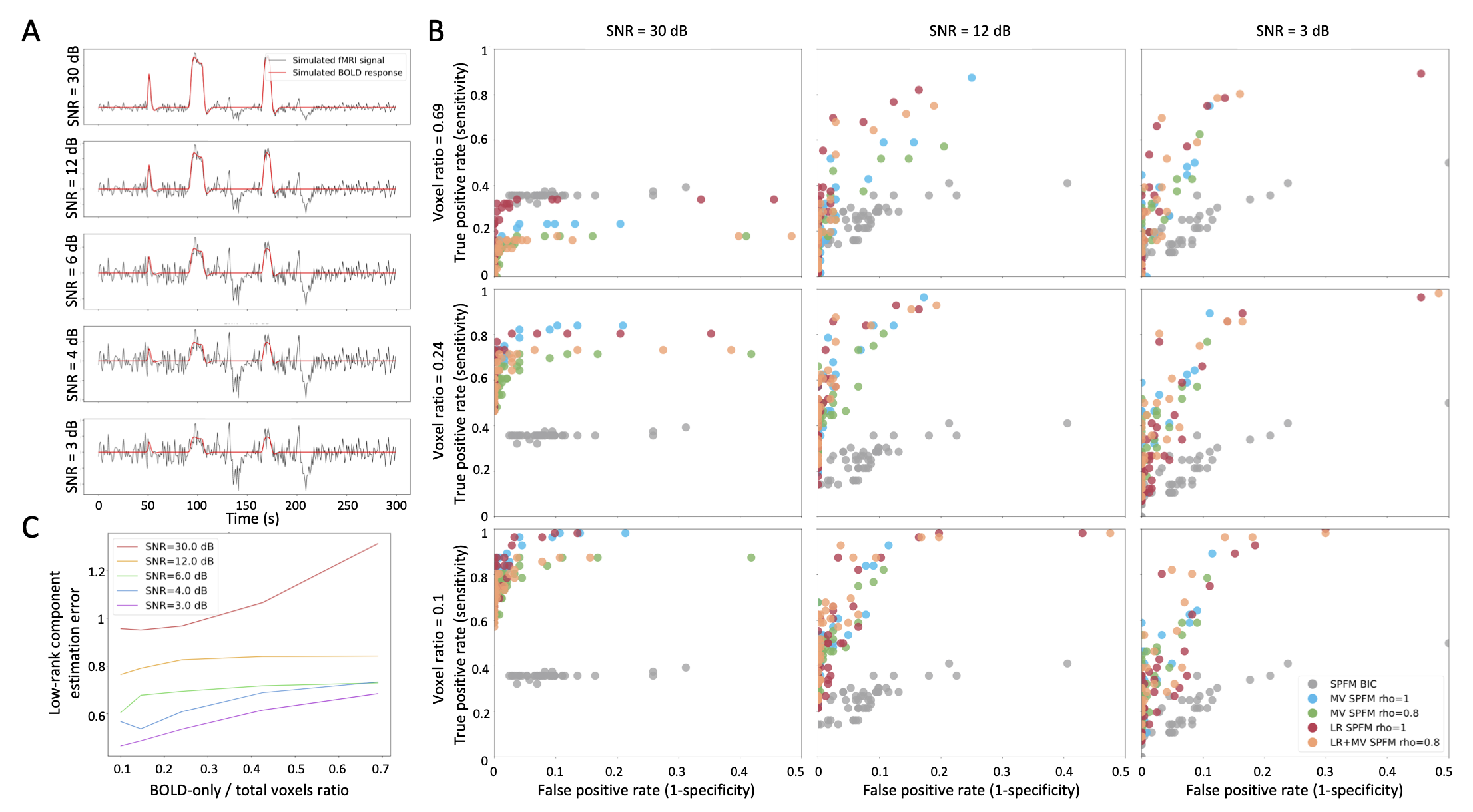
Figure 2:Simulation results. A) An example of the simulated signals for the different SNR conditions; B) ROC values for the estimation of the neuronal-related signal with: SPFM using BIC (SPFM BIC), SPFM with no low-rank estimation and no spatial regularization (SPFM, ), MV-SPFM with no low-rank estimation (MV-SPFM, ), the SPLORA-PFM algorithm with only the L1-norm (LR+SPFM, ), and the SPLORA-PFM algorithm (). C) Estimation error of the low-rank components for different ratios of BOLD/total number of voxels.
Figure 2B depicts the receiver operating characteristic (ROC) curves with the sensitivity and specificity rates for the estimation of the neuronal-related signal for each simulation scenario. Regardless of the simulated SNR and the BOLD/total voxels ratios, the ROC values demonstrate the proposed SPLORA-PFM algorithm achieves higher specificity and sensitivity than the original SPFM method, except for the highest BOLD/total number of voxels ratio and highest SNR where the multivariate nature of the model prevents the algorithm from fitting accurately each voxel. As expected, all variations of the proposed algorithm exhibit lower sensitivity as the SNR is reduced while maintaining the level of specificity. In addition, Figure 2C plots the error of the low-rank component estimate obtained with the SPLORA-PFM algorithm for , showing that its estimate improves with a lower BOLD/total voxels ratio.
Experimental Data¶
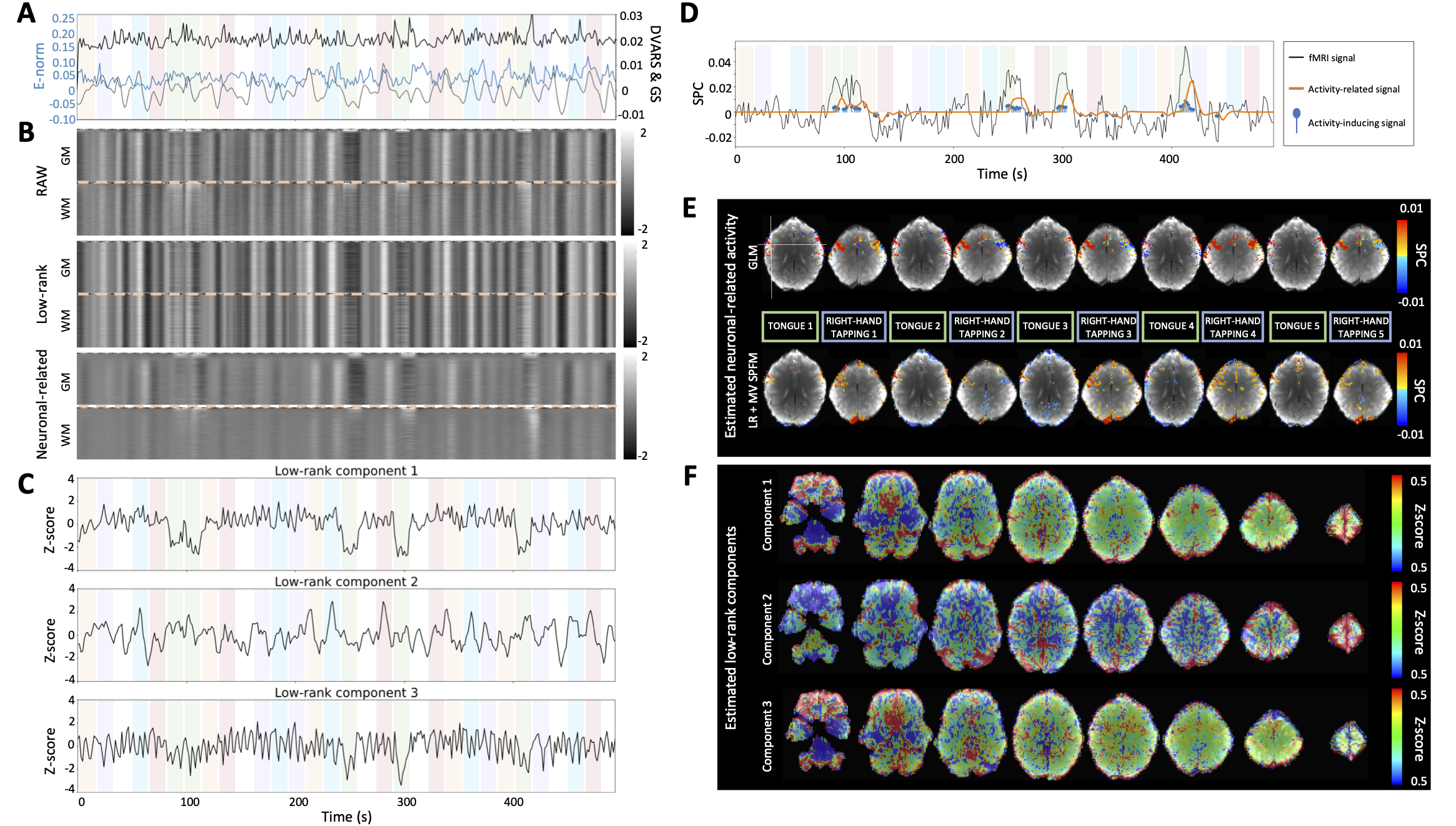
Figure 3:A) Euclidean norm of the motion displacements (E-norm) (blue), DVARS (black) and global (gray) signals of the fMRI data; B) Grayplots of gray matter (GM) and white matter (WM) of the preprocessed fMRI data, the estimated low-rank and neuronal-related components; C) Time series and F) maps of the estimated low-rank components; D) Time series and E) maps of representative single-trial neuronal-related (motor) activity. The color bands in the plots with the time series illustrate the timing of the different conditions.
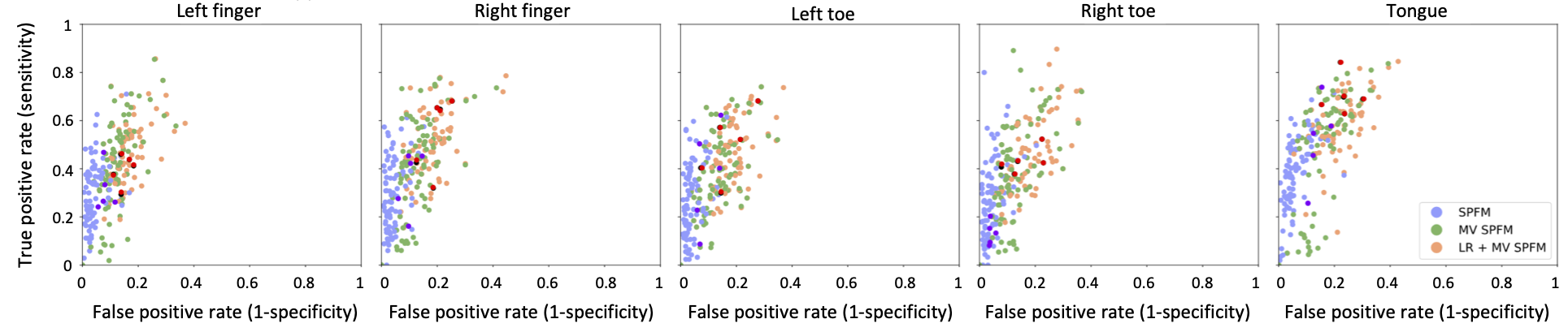
Figure 4:ROC values of the five conditions for the three algorithms tested: SPFM, MV-SPFM and SPLORA-PFM (red, dark-purple and dark-green dots correspond to the subject in Figure 3).
Figure 3A-F depict the results of the SPLORA-PFM algorithm in a representative dataset. For this subject and session, the proposed method estimated global low-rank components whose time series and spatial maps are shown in Figure 3C and F, respectively. Figure 3A shows the Euclidean norm of the motion displacements (E-norm), DVARS (the spatial root mean square of the data; Smyser et al. (2011), Power et al. (2012)) and the average global signal (GS) time series, whereas Figure 3B displays the grayplots of the preprocessed data (RAW), estimated low-rank component and estimated neuronal-related component in gray matter (GM) and white matter (WM) voxels. The first low-rank component captures signal fluctuations related to head movements and susceptibility artefacts during the “moving the tongue” condition, suggesting that the subject moved the head while performing the tongue movement task. The second low-rank component has a time series that closely follows the global signal and its spatial map actually delineates major arteries and draining veins, whereas the third component is clearly related to widespread physiological fluctuations. Among participants, the number of estimated low-rank components ranged between 1 and 5.
Furthermore, Figure 3D and Figure 3E illustrate the time series of the estimated neuronal-related signal for a representative voxel (see cross in the first map) and the maps for several individual events of the tongue movements and right hand finger tapping conditions, respectively. The SPLORA-PFM maps reveal clusters of activity in similar regions to those inferred with a traditional general linear model (GLM) analysis, which is aware of the timings of the events. The single-trial GLM activation maps are thresholded based on their t-statistic at a significance threshold of . Notably, the SPLORA-PFM maps still depict the tongue areas of the motor cortex bilaterally even though the timing of the first low-rank component also closely followed the tongue condition.
Finally, Figure 4 depicts the ROC values of the MV-SPFM and SPLORA-PFM, both using , and the original SPFM algorithm using the GLM maps of each event thresholded at a as the ground-truth. The ROC curves of the five motor task conditions show that both the MV-SPFM and the SPLORA-PFM approaches provide higher sensitivity at the cost of a reduced specificity, and that the higher complexity involved in estimating the low-rank component does not diminish the accuracy in deconvolving the neuronal-related component of the signal.
This work introduced a novel formulation for the deconvolution of BOLD fMRI data using a low rank and sparse algorithm that captures global fluctuations due to motion artefacts or physiological signals that typically reduce the accuracy of neuronal related estimates of currently used algorithms. The formulation described in this chapter was presented for single-echo acquisition and the spike model. However, it can be adapted straightforwardly for multi-echo Caballero-Gaudes et al., 2019 or the block model Karahanoğlu et al., 2013Cherkaoui et al., 2019Uruñuela et al., 2023 using the multi-echo and innovation signals described in Chapter 4: Whole-Brain Multivariate Deconvolution for Multi-Echo Functional MRI and respectively. Likewise, the selection of the regularization parameters , and ρ was done empirically here and could be further optimized using robust approaches such as stability selection Meinshausen & Bühlmann, 2010Uruñuela et al., 2020 as described in Chapter 3: Stability-Based Sparse Paradigm Free Mapping and Chapter 4: Whole-Brain Multivariate Deconvolution for Multi-Echo Functional MRI. Finally, future work will be directed towards evaluating the performance of SPLORA-PFM on resting-state data. Specifically, these evaluations will assess its effectiveness in mitigating the influence of commonly observed global fluctuations on activity-inducing signal estimates, since it is expected that SPLORA-PFM will exhibit superior performance in this regard compared to its performance on task fMRI data.
- Uruñuela, E., Moia, S., & Caballero-Gaudes, C. (2021, April). A Low Rank and Sparse Paradigm Free Mapping Algorithm For Deconvolution of fMRI Data. 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI). 10.1109/isbi48211.2021.9433821
- Power, J. D., Plitt, M., Laumann, T. O., & Martin, A. (2017). Sources and implications of whole-brain fMRI signals in humans. NeuroImage, 146, 609–625.
- Pruim, R. H. R., Mennes, M., van Rooij, D., Llera, A., Buitelaar, J. K., & Beckmann, C. F. (2015). ICA-AROMA: A robust ICA-based strategy for removing motion artifacts from fMRI data. NeuroImage, 112, 267–277. 10.1016/j.neuroimage.2015.02.064
- Kundu, P., Inati, S. J., Evans, J. W., Luh, W.-M., & Bandettini, P. A. (2012). Differentiating BOLD and non-BOLD signals in fMRI time series using multi-echo EPI. NeuroImage, 60(3), 1759–1770. 10.1016/j.neuroimage.2011.12.028
- Caballero-Gaudes, C., Moia, S., Panwar, P., Bandettini, P. A., & Gonzalez-Castillo, J. (2019). A deconvolution algorithm for multi-echo functional MRI: Multi-echo Sparse Paradigm Free Mapping. NeuroImage, 202, 116081. 10.1016/j.neuroimage.2019.116081