Functional Imaging of the Human Brain¶
For over a century, neuroscientists and neurophysiologists have dedicated their efforts to uncovering the functional organization of the brain. Through the use of various functional neuroimaging techniques with complementary temporal and spatial resolutions, they aim to reveal the neuro-anatomical localization and dynamic changes of brain activations.
While non-invasive electrophysiological techniques such as electroencephalography (EEG) or magnetoencephalography (MEG) excel in temporal resolution (10-100 ms), their spatial resolution is relatively poor (several mm or cm) Baillet et al., 2001Hämäläinen et al., 1993. In contrast, invasive electrophysiological techniques, including patch clamps Neher et al., 1978, single-unit or multi-unit recordings Arieli et al., 1995, and electrocorticography (ECOG) Miller et al., 2007Nir et al., 2008, offer high spatial resolution.
Functional magnetic resonance imaging (fMRI) and Positron Emission Tomography (PET) provide insight into cerebral blood flow and oxygen metabolism, indirectly associated with neural activations. With spatial resolutions in the order of millimeters, these techniques are capable of capturing activations in both cortical and deep brain structures, but their temporal resolution is limited by the sluggish dynamics of hemodynamic changes Dale & Halgren, 2001. fMRI offers higher temporal and spatial resolution compared to PET, making it more suitable for studying the temporal responses to short neuronal-related events. However, PET has the advantage of measuring well-defined physiological quantities such as cerebral blood flow (CBF), cerebral blood volume (CBV), or cerebral metabolic rate of oxygen or CMRO2 Fox et al., 1986Friston et al., 1993.
Functional MR spectroscopy (MRS) is an alternative method for metabolic imaging, offering quantitative measurements of functional changes in neurometabolite and neurotransmitter concentrations within a specific brain region. However, it is important to note that MRS has lower spatial and temporal resolutions compared to fMRI Morris, 1999. Typically, MRS is performed in a single voxel with an isotropic size of a few centimeters, or in multiple voxels using chemical shift imaging.
Lastly, optical diffusion imaging techniques, such as near infrared spectroscopy (NIRS) Kleinschmidt et al., 1996Villringer et al., 1993, diffusion optical tomography (DOT) White & Culver, 2010, or event-related optical signaling (EROS) Gratton & Fabiani, 2001Gratton et al., 1997, utilize an optical imaging device placed on the scalp to measure changes in cortical blood flow. However, due to the need for the light to penetrate through the skull, these techniques have lower spatial resolution compared to MR imaging techniques and are limited to studying the cortical surface. The temporal resolution of EROS is similar to MEG and EEG (in the order of milliseconds), while NIRS has a ten times higher temporal resolution to fMRI.A notable advantage of optical imaging is its lower cost and portability compared to other techniques such as MRI or MEG.
Blood Oxygen Level Dependent Functional MRI¶
In order to fully comprehend the assumptions and methods presented in this thesis, it is essential to review some basic concepts related to the physical and physiological basis of the blood oxygen-level dependent (BOLD) effect. MRI techniques offer a range of approaches to detect the increased metabolic demand associated with brain function. These include utilizing the BOLD contrast, changes in CBV using contrast agents such as gadolinium Dean et al., 1992, ferumoxytol Christen et al., 2012 or hyperoxic contrasts Bulte et al., 2007, and assessing CBF through arterial spin labeling techniques (ASL) Buxton, 2009. BOLD fMRI, introduced by Ogawa et al., 1990Ogawa et al., 1992, is particularly advantageous as it requires no exogenous contrast agent and exhibits higher sensitivity compared to CBF-based contrast, such as ASL. Consequently, it has gained widespread usage for functional brain imaging.
Physiological Basis of the BOLD Constrast¶
The signal contrast in BOLD fMRI images arises from variations in the local magnetic susceptibility, χ, caused by disparities in blood hemoglobin oxygen concentration. As local neuronal activity intensifies, there is a rise in oxygen consumption, leading to an augmented supply of oxygenated blood that diffuses passively through the capillary blood vessels to the tissue. When oxygen binds to hemoglobin (forming oxyhemoglobin), it exhibits slight diamagnetic properties relative to the tissue, causing the molecule to repel the magnetic field. In contrast, deoxygenated hemoglobin is paramagnetic compared to the tissue, attracting the magnetic field. Consequently, the magnetic field becomes distorted near deoxygenated red blood cells, creating higher local magnetic field gradients in the surrounding tissue, which results in spin dephasing. Reduced oxygenation amplifies the spin dephasing effect, shortening the tissue’s and diminishing the amplitude of the MR signal in -weighted images. Conversely, higher oxygen concentration aligns the susceptibility of the blood with that of the surrounding tissue, reducing the local magnetic field gradient, increasing , and raising the measured MR signal amplitude by a few percent. This forms the basis of BOLD fMRI, where changes in blood oxygenation serve as an intrinsic contrast mechanism in -weighted images, enabling the identification of cortical regions exhibiting functional activity characterized by increased oxygen demand and supply Bandettini et al., 1992Belliveau et al., 1991Kwong et al., 1992Ogawa et al., 1990Ogawa et al., 1992Turner et al., 1991.
Temporal Characteristics of the BOLD Signal: the Hemodynamic Response Function¶
The BOLD effect does not directly reflect neuronal activity, but rather measures the hemodynamic response associated with it Logothetis, 2008Logothetis et al., 2001. The relationship between the hemodynamic response and the underlying neuronal activity is complex involving dynamic changes in CBF, CBV and Buxton, 2009. After neuronal activity increases in a brain region, there is an initial decrease in blood oxygenation due to oxygen consumption which might cause a small initial dip in the hemodynamic response following the first second after the activation Ernst & Hennig, 1994Menon et al., 1995. Although this initial dip is not always observed in fMRI Behzadi & Liu, 2006Buxton, 2009Hu et al., 1997Hu et al., 1997, it is suggested that it maps more accurately the site of neural activity Duong et al., 2000Malonek & Grinvald, 1996. Afterwards, the local supply of oxyhemoglobin increases more than it is strictly demanded, probably to ensure a large oxygen gradient across capillary walls so that there is a high rate of transfer of oxygen or glucose to tissue Logothetis, 2008, generating a positive BOLD response due to an excess of oxyhemoglobin. Negative BOLD responses have also been observed associated with neuronal deactivations Shmuel et al., 2006. Regardless of the polarity of the response, the BOLD response peaks between 5 and 8 s after the activation starts and its amplitude depends on the type of stimulus and the magnetic field strength. For instance, for visual stimulation the signal change is 2-3% at 1.5T, 4-6% at 3T, 7-10% at 7T Zwaag et al., 2009. After the stimulus ceases, there is a return of the BOLD response to baseline, often followed by a post-stimulus undershoot due to an increase of deoxyhemoglobin which may last for several seconds until the response returns to baseline. The cause of the post-stimulus undershoot is also not completely understood, whether this is a vascular, neural or metabolic effect Buxton, 2009Chen & Pike, 2009. In summary, the time scale of the BOLD response is much slower than the time scale of neural activity and the return of the BOLD signal to baseline level after a short stimulus may occur more than 30 s from the stimulus onset. The temporal characteristics of the BOLD response are usually modelled by a hemodynamic response function (HRF). Figure 1 shows the shape of typical HRF, along with the initial dip for illustration of this effect. In this figure, the HRF plotted is the well-known canonical HRF Friston, 2007Friston et al., 1998, which is defined as the difference of two-gamma functions:
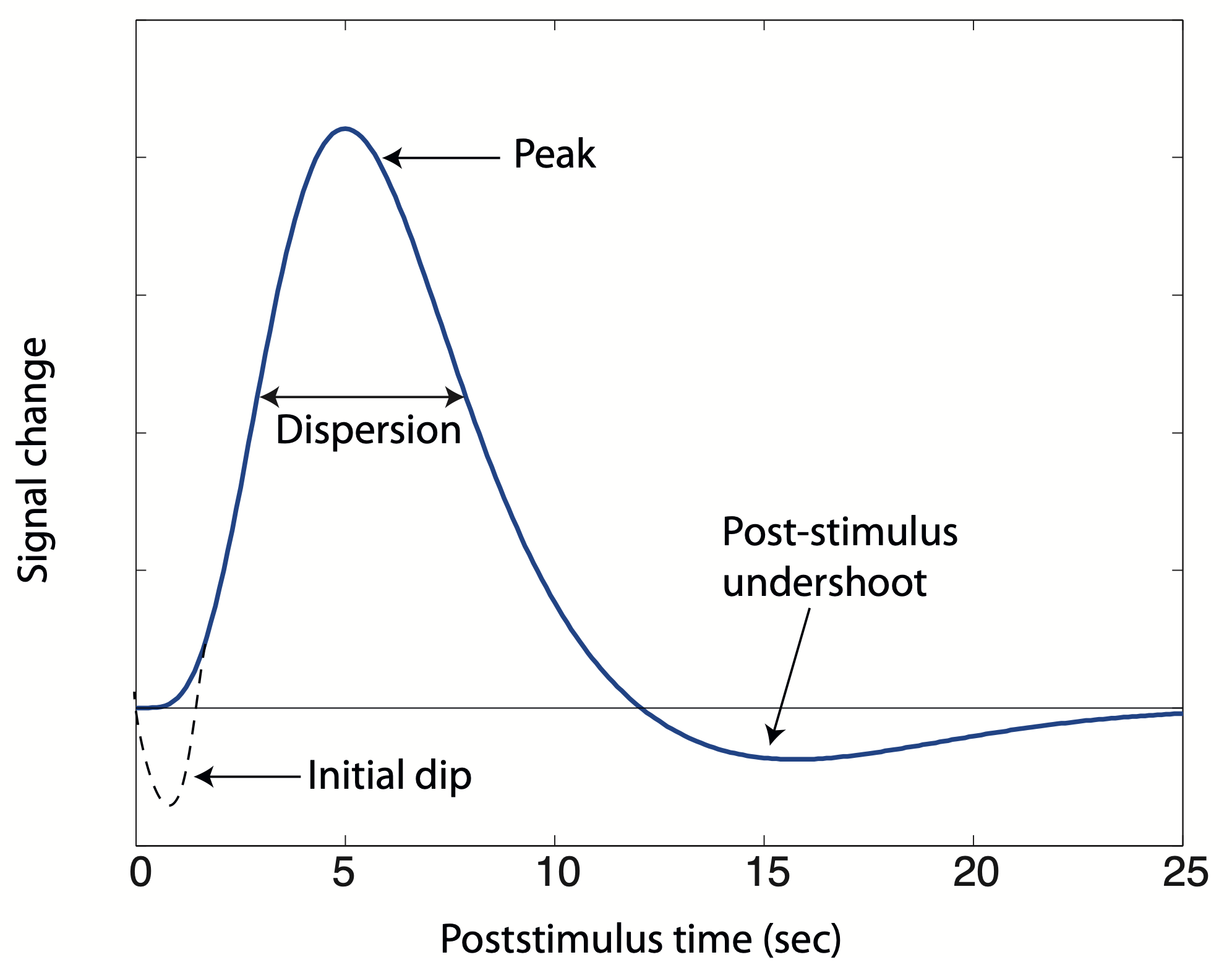
Figure 1:Temporal characterization of the haemodynamic response function. The shape in bold line corresponds to the canonical haemodynamic response function.
where the Gamma function is given by
The canonical HRF, as described in literature Friston, 2007, is characterized by specific parameters. These parameters include a time-to-peak of 6 s and dispersion of 1 s for the initial overshoot. Additionally, it has a time-to-peak of 16 s and dispersion of 1 s for the undershoot. The overshoot-undershoot ratio is approximately 6. However, it is important to note that the BOLD response exhibits variability across trials, brain regions, and subjects Aguirre et al., 1998Duann et al., 2002Handwerker et al., 2004McGonigle et al., 2000Smith et al., 2005. To account for this variability, alternative HRF shapes have been proposed in the scientific literature. These include single gamma functions Boynton et al., 1996Cohen, 1997, two-gamma functions with different HRF parameters Glover, 1999, Poisson functions Friston et al., 1994. and Gaussian functions Kruggel & Cramon, 1999Rajapakse et al., 1998.
Noise in BOLD fMRI¶
In addition to neuronal-related activity, the BOLD signal presents multiple sources of noise related to hardware-related artifacts and drifts, head motion, confounding physiological fluctuations Bianciardi et al., 2009Jorge et al., 2013 as well as image distortions related to data acquisition that should be accounted for and corrected during fMRI data preprocessing.
Motion and Other Artifacts¶
For instance, the images could present geometric distortions in the phase direction of the acquisition that can be removed by means of mapping field distorsions, either using field maps or using two images acquired in opposite phase-encoding directions, and then with a non-linear transformation of the fMRI volumes (e.g. TOPUP, Andersson et al., 2003Glasser et al., 2018). Also, fMRI images are typically acquired slice by slice and the difference in their time of acquisition can be compensated via slice timing correction, although this step can also introduce confounding effects in the data due to signal interpolation Parker & Razlighi, 2019. More generally, realigning all fMRI volume to a reference image can deal with part of the artifacts introduced by head motion Friston et al., 1994. However, this step does not remove the effect of motion completely Caballero-Gaudes & Reynolds, 2017.
The most straight-forward way to deal with signal artifacts is to model them as regressors of non-interest along with the task regressors (in tIA-fMRI) or to project them out of the fMRI data if there is no task paradigm, as in resting-state (RS) experiments. For instance, motion-related effects can be expressed as a set of the relative translations and rotation obtained during realignment, considering their first derivative and their squared transformation for up to 24 regressors for a better denoising Friston et al., 1994. Similarly, very low frequency trends due to hardware-related inestabilities can be modelled as a set of basis functions (e.g. using Legendre polynomials, Discrete Cosine Transform).
Furthermore, large deviations in the fMRI signal (e.g., spikes) caused by motion jerks and scanner noise can be removed through scrubbing or censoring Power et al., 2012. This process consists in identifying those fMRI volumes characterized by abrupt changes in the BOLD signal and removing or interpolating them. The identification can be performed by using summary metrics of motion, like Framewise Displacement Power et al., 2012, or by observing transient changes in the signal (DVARS, Power et al. (2012);Smyser et al. (2010)). However, it is important to notice that, if correctly accounted for, scrubbing could reduce the degrees of freedom in statistical analysis Mascali et al., 2021, leading to biases in second-level analysis between subjects that move too much and others, or introduce discontinuity in the signal itself, limiting the use of particular analyses dependent on signal continuity (e.g. ICA, see Caballero-Gaudes & Reynolds (2017)), and biasing the estimation of functional connectivity Mascali et al., 2021. Moreover, interpolating the signal could introduce spurious changes in the signal.
Another common approach to remove not only motion, but also other sources of noise, is based on data decomposition techniques. For instance, ICA can be leveraged to model, identify and remove motion artifacts as well as other sources of noise Behzadi et al., 2007Griffanti et al., 2014Muschelli et al., 2014Pruim et al., 2015Pruim et al., 2015Salimi-Khorshidi et al., 2014. Ideally, the best candidate to identify noisy timeseries would be temporal ICA, i.e., a decomposition in which the independence is forced in the temporal domain Glasser et al., 2018Smith et al., 2012. However, such approach is not feasible in a normal fMRI context since it would require the samples in time to be much higher than the samples in space Smith et al., 2012. Hence, spatial ICA is the most common application for fMRI decomposition, although this might lead to detect spurious components that contain both true BOLD signal and noise Caballero-Gaudes & Reynolds, 2017. Alternatively, several fMRI sessions could be concatenated to apply temporal ICA, although this approach would lead to the impossibility of removing session-specific noise. The challenging factor in adopting ICA for denoising is the classification of the independent components. Although manual classification is still the approach with the best outcome Griffanti et al., 2017, it is time consuming, it requires trained researchers, and the result is dependent on the observer. For this reason, different approaches for automatic classification of ICA components have been proposed in time, from full classifiers (FIX, Salimi-Khorshidi et al. (2014)) to approaches specifically targeting motion artifacts (ICA-AROMA, Pruim et al. (2015);Pruim et al. (2015)).
Alternatively, decomposing the signal of white matter (WM) and cerebrospinal fluid (CSF) into principal components and considering the first few (a technique called anatomical CompCor, see Behzadi et al. (2007)) can help retrieving proxies of motion-related artifacts and physiological fluctuations Behzadi et al., 2007Muschelli et al., 2014. In fact, it has been shown that CompCor can be more effective in denoising motion artifacts than ICA based techniques and censoring Mascali et al., 2021.
Noise in fMRI can also be reduced by using multi-echo (ME) acquisitions that sample the data at multiple successive echo times (TE). A weighted combination of the multiple echoes based on each voxel’s value Posse et al., 1999 or temporal signal-to-noise ratio Poser et al., 2006 can smear out random noise and enhance the sensitivity to the BOLD contrast. In fact, compared with single-echo data, this optimal combination Liu et al., 2022 can improve the mapping of neuronal activity at 3T Fernandez et al., 2017 and 7T Puckett et al., 2018, with results comparable to other preprocessing techniques requiring extra data such as RETROICOR Atwi et al., 2018. Optimal combination of multiple echo volumes can also improve sensitivity, specificity, repeatability and reliability of fMRI mapping Cohen et al., 2021Cohen & Wang, 2019.
Furthermore, assuming a monoexponential decay, the voxelwise fMRI signal acquired at a given echo time TE, i.e. , can be expressed in signal percentage change as:
where is the average signal at a given TE, represents non-BOLD related changes in the net magnetisation, represents BOLD-related susceptibility changes (and is the inverse of ), and denotes random noise Kundu et al., 2013Kundu et al., 2012. As the BOLD-related signal can be expressed as a function of the TE, whereas noise-related (i.e., non-BOLD) changes in the net magnetization are independent of TE, the information available in multiple echoes can be leveraged for the purpose of denoising. For example, in a dual-echo acquisition where the first TE is suficiently short, the first echo signal mainly captures changes in rather than in . It is then possible to remove artifactual effects, through voxelwise regression, from the second echo signal acquired at a longer TE with appropriate BOLD contrast Bright & Murphy, 2013.
Collecting more echoes opens up the possibility to leverage ICA and automatically classifying independent components into BOLD-related (i.e., describing fluctuations with a linear TE-dependency) or noise (i.e., independent of TE, related to non-BOLD fluctuations in the net magnetization ), an approach known as ME independent component analysis (ME-ICA, Kundu et al. (2013);Kundu et al. (2012);Kundu et al. (2017)). Compared to single-echo data denoising, MEICA can improve the mapping of task-induced activation DuPre et al., 2021Gonzalez-Castillo et al., 2016Lombardo et al., 2016, for example in challenging paradigms with slow-varying stimuli Evans et al., 2015 or language mapping and laterality Amemiya et al., 2018. It also outperforms single-echo ICA-based denoising of resting-state fMRI data Dipasquale et al., 2017Lynch et al., 2020, and provide more effcient and reliable functional connectivity mapping in individual subjects Lynch et al., 2020 and in brain regions where traditional single-echo acquisitions offer reduced signal-to-noise ratio, such as the basal forebrain Markello et al., 2018. Finally, ME-ICA also enhances the deconvolution of neuronal-related signal changes Caballero-Gaudes et al., 2019.
Physiological Artifacts¶
When employing BOLD fMRI as an intrinsic contrast to investigate neural correlates, it becomes essential to decouple the neurovascular coupling. In this context, physiological signals may introduce noise, requiring their modeling to account for and minimize their associated variance during preprocessing or data analyses Caballero-Gaudes & Reynolds, 2017Liu, 2016. The principal frequencies characterising physiological signals like cardiac pulse and respiration are in a different band compared to those of the neural-related BOLD signal: namely, the primary component of cardiac related fluctuations are around 1 Hz, while the respiratory related ones are around 0.3 Hz. Thus, if the temporal sampling is high enough, a simple band-pass filter could easily remove their confounding effects Biswal et al., 1995Chuang & Chen, 2001Lowe et al., 1998. The downside is that this approach will remove the BOLD-related signal frequencies in the same range as well, and it will not remove the impact of physiological frequencies in the same range as the BOLD signal Caballero-Gaudes & Reynolds, 2017. This is especially true if the temporal sampling is low and the physiological signal is aliased in the BOLD-related frequency range. Moreover, physiological signal, and respiration in particular, has an impact on other sources of noise, like magnetic field perturbation Raj et al., 2001, and motion Fair et al., 2020Pais-Roldán et al., 2018Power et al., 2019 that should be taken into account and removed Gratton et al., 2020.
An easy way to remove such perturbations is to remove the average brain signal (also called global signal), since it is often considered as a proxy of the combined impact of different sources of noise, especially related to movement or physiological in nature. However, its removal is controversial, since it can heavily alter the interpretation of BOLD fMRI Power et al., 2017. For this reason, Power et al. (2018) proposed to decompose fMRI data in low and high rank components, and to consider the first few low rank components timeseries as noise. This technique, called GODEC, showed improved denoising of fMRI data after ME-ICA Power et al., 2018Zhou & Tao, 2011.
As an alternative, the average signal in the white matter (WM) and cerebrospinal fluid (CSF) can be used as a proxy of physiological noise, since no neural-related signal is present in these tissues, that are conversely dominated by cardiac pulsatility and respiration Anderson et al., 2011Jo et al., 2010, although more recently Attarpour et al. (2021) showed that the average CSF does not represent cardiac fluctuations properly. Specifically, ICA based decomposition can be set up to retrieve physiological-related signals, both in space (CORSICA, Perlbarg et al. (2007)) and in time (PESTICA, Beall & Lowe (2007)).
An alternative to data-driven approaches consists in acquiring physiological signals such as cardiac pulse and respiration effort during the imaging session, opening up the possibility to adopt more model-based approaches to deal with physiological noise. For instance, it is possible to estimate the frequencies of the amplitude envelope of cardiac and respiratory signals, and then selectively filter them from fMRI data Biswal et al., 1996. However, the main frequency and the harmonics of physiological fluctuations are usually aliased with the spectra of BOLD components with neurobiological relevance, and bandpass filtering would remove them as well.
Alternatively, it is possible to use the measured cardiac and respiratory signals to model their pseudo-periodic fluctuation that are phase-locked to the fMRI signal. Cardiac and respiratory phases can be estimated from signal recordings, then their Fourier expansion can be removed from the data in a slice-dependent manner at the beginning of the preprocessing, an approach known as RETROICOR, Glover et al. (2000). However, RETROICOR does not remove completely the effect of physiological signal from the data, especially regional low frequency effects that vary between brain regions Birn et al., 2006Chang et al., 2009Shmueli et al., 2007.
Noticeably, slow variations in the heart rate (HR, Shmueli et al. (2007)) and the respiration volume per time (RVT, Birn et al. (2006)) have been applied successfully to denoise BOLD signal from physiological fluctuations after RETROICOR, especially when convolved with a modelled response function, cardiac Chang et al., 2009 or respiratory Birn et al., 2008. Various alternatives to RVT to improve breathing-related denoising have been proposed, either to simplify their calculation, that is normally based on the peak detection in the respiratory signal, or to improve the detection of particular changes in the respiratory signal. For instance, Chang & Glover (2009) proposed to simply use the standard deviation of the respiratory signal, thus avoiding peak detection. Power et al. (2018) suggested to compute the standard deviation of the respiratory envelope in small windows to be more susceptible to breathing changes. More recently, Harrison et al. (2021) showed that applying an Hilbert transform to compute RVT improves the characterisations of breathing rhythms and the detection of deep breaths. Although the regions impacted by slow variations in cardiac rate and breathing patterns frequently overlap Chang et al., 2009Kassinopoulos & Mitsis, 2019, HR and RVT regressor can be used together for better performance Chang et al., 2009.
Another physiological confound related to RVT consists in spontaneous changes in arterial CO2, called poikilocapnia, which act as a vasoactive process. These fluctuations have been corroborated with Transcranial Doppler ultrasound (TCD) and induce low frequency fluctuations in the BOLD signal. If they are not accounted for, they can induce a bias in the signal estimation in up to a fifth of the cortex Wise et al., 2004. The pattern of biases induced by poikilocapnia has been found comparable to that of RVT Chang & Glover, 2009, although accounting for the latter is not suffcient to explain all the variability induced by the former Golestani et al., 2015. However, the fact that BOLD signal is susceptible to CO2 fluctuations can be conversely seen as an advantage, and used to image cerebral physiology Pinto et al., 2021Zvolanek et al., 2023Moia et al., 2021.
fMRI Data Analysis¶
Task fMRI¶
Conventionally, the analysis of task fMRI data consists of solving a generalized liner model (GLM) analysis. Since researchers have access to the timings of the stimuli, it is possible to model the expected BOLD response to the stimuli and then fit the model to the data. For instance, the onsets of the expected neuronal activity for a given condition can be modeled as an indicator function (e.g., Dirac functions for event-related designs, or box-car functions for block-designs) convolved with the HRF , sampled at the resolution of the TR Friston et al., 2008Friston et al., 1998Boynton et al., 1996Cohen, 1997:
Hence, the vector represents the regressor that models the hypothetical BOLD response for an experimental condition. Then, different regressors either modeling conditions of interest or signals of non interest (e.g., noise-related signals) can be added as the columns of the design matrix , where is the number of regressors, which leads to the well-known GLM equation:
where the voxel timecourse is explained by a linear combination of the regressors in , weighted by the regression coefficients , and the residual error or noise . The GLM can be solved using ordinary least squares (OLS) under the assumption that the noise is independent and identically distributed (i.i.d.) Gaussian. Hence, the estimates of neuronal activity corresponding to the task conditions are obtained minimizing the residual sum of squares between the fitted model and the measured voxel timecourse. Usually, the number of regressors is much smaller than the number of samples, and thus the GLM is an overdetermined problem. In this case, the solution can be obtained without the need for additional constraints or assumptions Henson & Friston, 2007. It is important to note that the GLM only provides estimates of the neuronal activity associated with the timings of the modelled stimuli.
Resting-State fMRI¶
Conversely, fMRI data analysis in unconstrained conditions such as when subjects lying still in the scanner without performing any specific task, i.e. in resting-state, poses a challenge for the application of GLM-based approaches due to the absence of an experimental paradigm that can be used to model the expected BOLD response. Given the increasing popularity of resting-state fMRI in the past decade, various data-driven approaches have emerged to address the analysis of this type of data.
Seed correlation analysis is widely recognized as the predominant approach for examining resting-state fMRI data due to its frequent utilization in the computation of functional connectivity (FC) patterns. It involves measuring the pairwise Pearson correlation between the timecourse of different voxels or regions of the brain, presenting the brain’s interregional connections or edges in the form of a FC matrix. Each edge in the matrix represents the strength or intensity of the functional connectivity between two regions. In fact, FC has been extensively utilized to investigate the arrangement of large-scale brain networks Salvador et al., 2005Yeo et al., 2011Margulies et al., 2016, as well as to partition smaller brain structures like the thalamus and striatum Martino et al., 2008Yuan et al., 2015Tian et al., 2020. Notably, FC exhibits subject-specific variations to such an extent that it can serve as a means of individual identification within a diverse population. Numerous studies have demonstrated the presence of distinct and reliable subject-specific features, commonly referred to as “fingerprints,” within the FC matrix Miranda-Dominguez et al., 2014Finn et al., 2015Finn et al., 2017Vanderwal et al., 2017Waller et al., 2017Amico & Goñi, 2018Peña-Gómez et al., 2017Horien et al., 2019Jalbrzikowski et al., 2020Jo et al., 2021. In fact, these fingerprints have been associated with predictive insights into cognition Cole et al., 2012Rosenberg et al., 2015Yamashita et al., 2018Fong et al., 2019Rosenberg et al., 2020Sripada et al., 2019, personality traits Adelstein et al., 2011Hsu et al., 2018Nostro et al., 2018Dubois et al., 2018, age Dosenbach et al., 2010Cabral et al., 2017Liem et al., 2017Nielsen et al., 2018, and disease phenotype Lynall et al., 2010Plitt et al., 2015Emerson et al., 2017Lake et al., 2019Svaldi et al., 2021.
Functional connectivity patterns offer a valuable insight into the connectivity among brain regions over a timecourse of data. However, they only provide a single snapshot and do not capture how this connectivity evolves over time, thereby neglecting the dynamics of functional connectivity Allen et al., 2012Di & Biswal, 2020Hutchison et al., 2013. Dynamic functional connectivity (dFC) in resting-state is commonly investigated using sliding-window approaches Allen et al., 2012Hutchison et al., 2013Preti et al., 2017Lurie et al., 2020. A sliding-window FC analysis yields a series of time-varying matrices, which are often effectively condensed into a few distinct brain states using clustering techniques Hutchison et al., 2013. In particular, it has been shown that dFC correlates with underlying neural activity Tagliazucchi et al., 2012Thompson et al., 2013Keilholz, 2014 and behavior Liégeois et al., 2019. Furthermore, studies have demonstrated that dynamic connectivity fluctuations exhibit lower variability between regions within the same functional networks, while showing higher variability between regions from different networks Fu et al., 2017. This pattern results in an overall negative correlation with stationary functional connectivity Thompson & Fransson, 2015Zhang et al., 2018. However, due to the unconstrained nature of resting-state fMRI, it becomes challenging to ascertain the functional significance of the obtained dynamic connectivity estimates versus their potential derivation from noise Lindquist et al., 2014. Recently, researchers have also explored dynamic connectivity in the context of participants exposed to complex stimuli, such as movie clips Di & Biswal, 2020. The utilization of movie stimuli offers the advantage of comparing the time course of dynamic connectivity across participants. If there is a high degree of inter-individual similarity Hasson et al., 2004Nastase et al., 2019, it may suggest that the observed dynamics of brain patterns is functionally meaningful and relevant to stimulus processing.
In addition, ongoing developments in the field of dFC methods allow for their operation within individual timeframes. One such method is the use of instantaneous phase synchrony (PS), which provides a reliable measure of connectivity with maximal temporal resolution, comparable to correlation-based methods. Comparing these patterns over time can be achieved by calculating the percentage of time points that exhibit significant phase synchronization throughout the entire scanning duration Glerean et al., 2012. Alternatively, the leading eigenvectors can be studied for this purpose Cabral et al., 2017. Another approach involves employing wavelet transform coherence to explore nonstationary changes in the coupling between fMRI time series. This method calculates coherence and phase lag between two time series as a function of both time and frequency. The selected time series could be either seed timecourses Chang & Glover, 2010 or timecourses of an ICA Yaesoubi et al., 2015. Similar to the sliding window approach, temporal dynamics can be identified through the application of clustering algorithms (e.g. k-means) Yaesoubi et al., 2015Cabral et al., 2017.
Another alternative method for analyzing single timeframe resting-state fMRI data involves investigating co-activation patterns (CAP) Tagliazucchi et al., 2012Liu et al., 2013Chen et al., 2015Liu et al., 2018. Unlike the phase synchrony approach, CAP analyses focus on identifying simultaneous occurrences of BOLD signal peaks or troughs in different brain regions, disregarding the phase of the signal, assuming that the relationship between the BOLD signal and neural activity is attributed to these brief, transient and sparse co-activation events Zhang et al., 2020. Typically, CAP analyses employs k-means clustering to group the identified events into distinct CAPs, enabling the identification of temporal dynamics that can potentially be compared to other time-varying resting-state methods such as sliding-window correlation in dFC and PS. Still, the basic approach in CAPs uses the fMRI signal as its input, which is thus subject to the temporal blurring of the hemodynamic response. This phenomenon could lead to the simultaneous co-activation of multiple regions, despite their distinct initial onsets, potentially indicating their association with different components Rangaprakash et al., 2018. In other words, due to temporal variations in the the hemodynamic response, the BOLD signals of several brain regions might exhibit simultaneous peaks despite the fact that their underlying neuronal activity might have different timings.
To address this potential ambiguity, these neuronal-related events can also be identified by means of hemodynamic deconvolution approaches that remove the blurring effect of the hemodynamic response from the time series Gaudes et al., 2013Karahanoğlu et al., 2013Petridou et al., 2013. Hemodynamic deconvolution is commonly used in investigating psychophysiologic interactions (PPI) within task-based functional connectivity studies Gerchen et al., 2014Gitelman et al., 2003 as well as in resting-state fMRI Di & Biswal, 2015. Recent deconvolution techniques, in contrast to classical PPI analysis, employ sparsity-promoting estimators that assume the dynamics of spontaneous brain activity can be characterized by sparse BOLD events Gaudes et al., 2013Karahanoğlu et al., 2013Petridou et al., 2013Uruñuela et al., 2023. These approaches are akin to methods using point process analysis to examine sparse BOLD events Tagliazucchi et al., 2012, and will be the focus of this thesis as introduced in the next section.
Mixing the ideas of hemodynamic deconvolution and co-activation patterns, Karahanoğlu & Van De Ville (2015) proposed a new approach named innovation-driven co-activation patterns (iCAPs) that is based in transients (i.e. innovations) of the fMRI signal, rather than its peaks. This technique employs the hemodynamic deconvolution algorithm of Total Activation Karahanoğlu et al., 2013 to estimate the underlying neural activity prior to applying the CAP analysis, and therefore encode information about transient changes in the signals originating the BOLD timecourses. Evidence from the study conducted by Karahanoğlu & Van De Ville (2015) using the framework revealed that well-known resting-state networks, including the default mode network, can be subdivided into multiple subsystems with distinct temporal dynamics. This suggests the existence of functionally diverse subnetworks within these networks. Furthermore, by backprojecting iCAPs to deconvolved fMRI volumes, it becomes possible to reconstruct iCAP time courses and assess temporal overlaps between different patterns Zoller et al., 2019. Notably, it has been observed that, on average, 3 to 4 iCAPs overlap in time, and the associated brain activity persists for 5-10 seconds. This finding may explain the necessity of using a window length of at least 20 seconds to obtain reliable inferences when employing a sliding window approach Karahanoğlu & Van De Ville, 2015Preti et al., 2017.
Another way to investigate functional connectivity is by identifying quasi-periodic patterns (QPP) of connectivity, which typically persist for approximately 20 seconds in humans. A repeated-template-averaging algorithm can be employed to detect these patterns in spatiotemporal segments Majeed et al., 2011. This approach involves iteratively computing sliding window correlations and averaging similar segments of BOLD timepoints until convergence is achieved. As a result, a spatiotemporal averaged template of BOLD dynamics is obtained. Interestingly, these templates often reveal patterns that reflect global signal fluctuations, representing the average time course of the BOLD signal across the entire brain Yousefi et al., 2018Bolt et al., 2022. Furthermore, these QPPs have been found to correlate with local infraslow neural activity Thompson et al., 2014. The predominant QPP typically exhibits a sequence characterized by a transition from strong activation of the default mode network (DMN) and deactivation of sensory and attention networks to the opposite state, with DMN deactivation and activation of sensory and attention networks Abbas et al., 2019Yousefi & Keilholz, 2021.
Finally, notice that when the FC strengh between two timecourses (i.e. the edges of the FC matrix) is measured as the pairwise Pearson’s correlation, this can be exactly defined in terms of its frame-wise contributions. Therefore, instead of detecting significant instances of FC change from voxel timecourses, these can be identified when multiple timecourses exhibit extreme signal changes simultaneously (i.e. co-activation) Esfahlani et al., 2020Faskowitz et al., 2020. These edge-centric FC (eFC) approach has recently gained notable popularity in brain imaging and neuroscience, showing that eFC offers large replicability, stability within individuals across multiple scanning sessions, and reliability across datasets Faskowitz et al., 2020. Moreover, clustering the eFC has revealed overlapping brain communities that hold promise for studying cognition and behavior beyond the limitations of traditional disjoint brain parcellations. However, the main findings of the edge-centric analyses can be derived from a node-centric FC perspective nFC (i.e., the commonly-used FC matrix) under a static null hypothesis that disregards temporal correlations Novelli & Razi, 2022. Consequently, the findings obtained with eFC-based methods can be also applied to nFC-based approaches, such as (i)CAPs or hemodynamic deconvolution, providing a similar set of volumes with large co-activations are used for subsequent analyses.
Introduction to the Chapters and Aim of the Studies¶
The aim of this thesis is to develop novel methods for the hemodynamic deconvolution of fMRI data and apply them in resting-state, naturalistic paradigms, and clinical-based studies.
In Chapter 2 the theoretical background of hemodynamic deconvolution is presented with a focus on the two different mathematical formulations, i.e., analysis and synthesis, and the associated algorithms: Total Activation and Paradigm Free Mapping. This chapter will aim to compare the two methods (that work at the individual voxel level), assess whether they are equivalent, and how they compare with Coactivation Pattern analysis.
Chapter 3 addresses the challenge of determining adequate regularization parameters for hemodynamic deconvolution. The method of stability selection is proposed as a solution to circumvent the need for manual parameter selection. Furthermore, a novel metric based on the area of the stability path is introduced that quantifies the likelihood of a neuronal-related event occurring at a specific voxel and timepoint.
Chapter 4 presents an extension of the hemodynamic deconvolution problem to a multivariate formulation, which enables the identification of neuronal-related events that are shared across multiple voxels. The method is presented and applied to single-echo and multi-echo fMRI data, employs the stability selection method introduced in Chapter 3 for parameter selection, and is validated with a comparison with a generalized linear model as the ground truth. Furthermore, the performance of this novel multivariate method is compared with its univariate counterpart, as well as with another semi-blind multivariate deconvolution technique that has been proposed in the literature, named Hemolearn.
Building upon this multivariate formulation, Chapter 5 introduces a novel method for the simultaneous identification of the neuronal-related events in multiple subjects. The technique is presented as a new tool that allows for the analysis of naturalistic fMRI data at the finest spatial and temporal resolution, unlike other methods that have been proposed in the literature so far. The method is validated in simulated and real data, and its performance is corroborated by correlating the identified neuronal-related events with different features of the movies the subjects watched during the fMRI acquisition.
A novel method, presented in Chapter 6, introduces a paradigm free mapping approach that effectively identifies and decouples global fluctuations in the BOLD signal during the deconvolution process. Compensating for these global events during data preprocessing is challenging, and they can be mistakenly interpreted as neuronally related due to their temporal signature closely resembling the assumed HRF in the deconvolution model. Hence, this decoupling is crucial for optimizing deconvolution approaches, as the estimation accuracy can be significantly compromised by widespread signal changes caused by head jerks, hardware artifacts, or non-neuronal physiological events (e.g., deep breaths).The method is validated in simulated and real data, and its performance is compared with a GLM analysis as the ground truth.
Finally, Chapter 7: Conclusion and future directions summarizes the main findings of this thesis and outlines future directions for research.
List of Contributions¶
Part of the work described in this thesis has been published in peer-reviewed journals and presented in conferences. The following list summarizes the main contributions of this thesis:
Journal and Conference Articles¶
- Chapter 2: Uruñuela, E., Bolton, T. A., Van De Ville, D., & Caballero-Gaudes, C. (2023). Hemodynamic Deconvolution Demystified: Sparsity-Driven Regularization at Work. Aperture Neuro, vol. 3, 1-25.
- Chapter 3: Uruñuela, E., Jones, S., Crawford, A., Shin, W., Oh, S., Lowe, M., & Caballero-Gaudes, C. (2020, July). Stability-Based Sparse Paradigm Free Mapping Algorithm for Deconvolution of Functional MRI Data. In 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC) (pp. 1092-1095).
- Chapter 4: Uruñuela, E., Gonzalez-Castillo, J., Zheng, C., Bandettini, P., & Caballero-Gaudes, C. (2023). Whole-Brain Multivariate Hemodynamic Deconvolution for fMRI with Stability Selection. Medical Image Analysis, 103010.
- Chapter 6: Uruñuela, E., Moia, S., & Caballero-Gaudes, C. (2021, April). A Low Rank and Sparse Paradigm Free Mapping Algorithm for Deconvolution of fMRI Data. In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI) (pp. 1726-1729).
Conference Abstracts¶
- Uruñuela, E., Sava-Segal, C., Leung, M., Finn, E.S., Caballero-Gaudes, C. A Multi-Subject Deconvolution Algorithm for the Analysis of Naturalistic fMRI Data. 3rd Annual meeting of the Iberian Chapter of the International Society of Magnetic Resonance in Medicine (2023), Valladolid, Spain.
- Uruñuela, E., Sava-Segal, C., Leung, M., Finn, E.S., Caballero-Gaudes, C. A Multi-Subject Deconvolution Algorithm for the Analysis of Naturalistic fMRI Data. 32nd Annual Meeting of the International Society of Magnetic Resonance in Medicine (2023), Toronto, Canada.
- Uruñuela, E., Moia, S., Caballero-Gaudes, C. A Multi-Echo Low-Rank and Sparse Method to Estimate Neuronal Signal with Less Global Signal Bias. 2nd Annual meeting of the Iberian Chapter of the International Society of Magnetic Resonance in Medicine (2022), Lisbon, Portugal.
- Uruñuela, E., Moia, S., Caballero-Gaudes, C. A Multi-Echo Low-Rank and Sparse Method to Estimate Neuronal Signal with Less Global Signal Bias. 28th Annual Meeting of the Organization for Human Brain Mapping (2022), Glasgow, UK.
- Uruñuela, E., Ferrer, V., Caballero-Gaudes, C. Blind Estimation of Neuronal-Related Activity in fMRI Informed by Co-Fluctuations of Brain Regions. 28th Annual Meeting of the Organization for Human Brain Mapping (2022), Glasgow, UK.
- Uruñuela, E., Moia, S., Caballero-Gaudes, C. A Multi-Echo Low-Rank and Sparse Algorithm That Reduces the Bias of Global Fluctuations on the Estimation of Neuronal Signal. 31st Annual Meeting of the International Society of Magnetic Resonance in Medicine (2022), London, UK.
- Uruñuela, E., Moia, S., Caballero-Gaudes, C. Synthesis-Based Paradigm Free Mapping and Analysis-Based Total Activation Operate Identically. 27th Annual Meeting of the Organization for Human Brain Mapping (2021), Virtual.
- Uruñuela, E., Moia, S., Caballero-Gaudes, C. Simultaneous Blind Estimation of Global Fluctuations and Neuronal-Related Activity from fMRI Data. 1st Annual meeting of the Iberian Chapter of the International Society of Magnetic Resonance in Medicine (2021), Virtual.
- Uruñuela, E., Moia, S., Caballero-Gaudes, C. Synthesis-Based Paradigm Free Mapping and Analysis-Based Total Activation Are Identical For Temporal Deconvolution of fMRI Data. 1st Annual meeting of the Iberian Chapter of the International Society of Magnetic Resonance in Medicine (2021), Virtual.
- Uruñuela, E., Moia, S., Caballero-Gaudes, C. fMRI deconvolution with Synthesis-Based Paradigm Free Mapping and Analysis-Based Total Activation Operate Identically. 30th Annual Meeting of the International Society of Magnetic Resonance in Medicine (2021), Virtual.
- Uruñuela, E., Moia, S., Caballero-Gaudes, C. Low-Rank and Sparse Simultaneous Blind Estimation of Global Fluctuations and Neuronal-Related Activity from fMRI Data. 30th Annual Meeting of the International Society of Magnetic Resonance in Medicine (2021), Virtual.
- Uruñuela, E., Jones, S., Crawford, A., Shin, W., Oh, S., Lowe, M., Caballero-Gaudes, C. Improving Deconvolution of fMRI Signal with Sparse Paradigm Free Mapping Using Stability Selection. 26th Annual Meeting of the Organization for Human Brain Mapping (2020), Virtual.
- Uruñuela, E., Moia, S., Gonzalez-Castillo, J., Caballero-Gaudes, C. Deconvolution of Multi-Echo Functional MRI Data with Multivariate Multi-Echo Sparse Paradigm Free Mapping. 27th Annual Meeting of the International Society of Magnetic Resonance in Medicine (2019), Montreal, Canada.
- Baillet, S., Mosher, J. C., & Leahy, R. M. (2001). Electromagnetic brain mapping. IEEE Signal Processing Magazine, 18(6), 14–30. 10.1109/79.962275
- Hämäläinen, M., Hari, R., Ilmoniemi, R. J., Knuutila, J., & Lounasmaa, O. V. (1993). Magnetoencephalography—theory, instrumentation, and applications to noninvasive studies of the working human brain. Reviews of Modern Physics, 65(2), 413–497. 10.1103/revmodphys.65.413
- Neher, E., Sakmann, B., & Steinbach, J. H. (1978). The extracellular patch clamp: A method for resolving currents through individual open channels in biological membranes. Pflügers Archiv European Journal of Physiology, 375(2), 219–228. 10.1007/bf00584247
- Arieli, A., Shoham, D., Hildesheim, R., & Grinvald, A. (1995). Coherent spatiotemporal patterns of ongoing activity revealed by real-time optical imaging coupled with single-unit recording in the cat visual cortex. Journal of Neurophysiology, 73(5), 2072–2093. 10.1152/jn.1995.73.5.2072
- Miller, K. J., denNijs, M., Shenoy, P., Miller, J. W., Rao, R. P. N., & Ojemann, J. G. (2007). Real-time functional brain mapping using electrocorticography. NeuroImage, 37(2), 504–507. 10.1016/j.neuroimage.2007.05.029